Q.43 Cash Award Qn posted on 01.10.2025

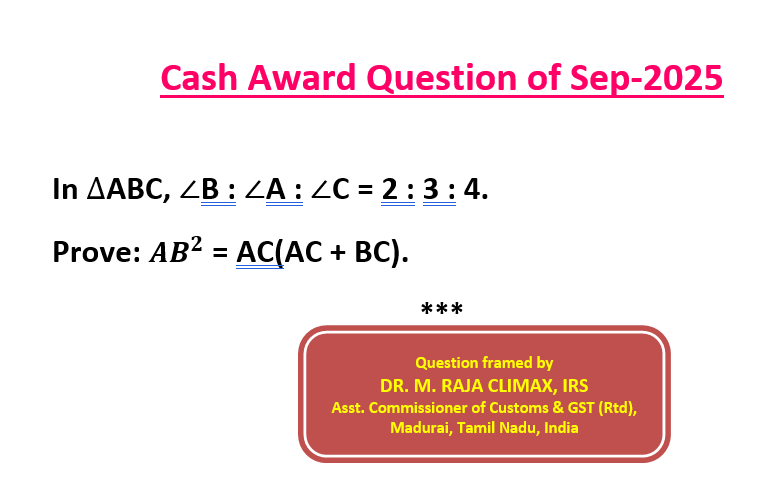
42. Cash Award Question posted on 01.09.2025
41. Cash Award Qn posted on 01.08.2025

Q.40 Cash Award Qn posted on 01.07.2025

Q.38 Cash Award Qn posted on 01.06.2025

Q.37 Cash Award Qn posted on 01.05.2025

Q.36 Cash Award Qn posted on 01.04.2025

Q.35 Cash Award Qn posted on 01.03.2025

Q.34 Cash Award Qn posted on 01.02.2025

Q.33 Cash Award Qn posted on 01.01.2025

Q.32 Cash Award Qn posted on 01.12.2024

Q.31 Cash Award Qn posted on 01.11.2024

Q.30 Cash Award Qn posted on 01.10.2024
.jpeg)
Q.29 Cash Award Qn posted on 01.09.2024

Q.28 Cash Award Math Rider posted on 01.08.2024

Q.27 Cash Award Math Rider posted on 01.07.2024

Q.26 Cash Award Math Rider posted on 01.06.2024

Q.25 Cash Award Qn posted on 01.05.2024

Q.24 Cash Award Qn posted on 01.04.2024

Q.23 Cash Award Math Rider posted on 01.03.2024

Q.22 Cash Award Math Rider posted on 01.02.2024
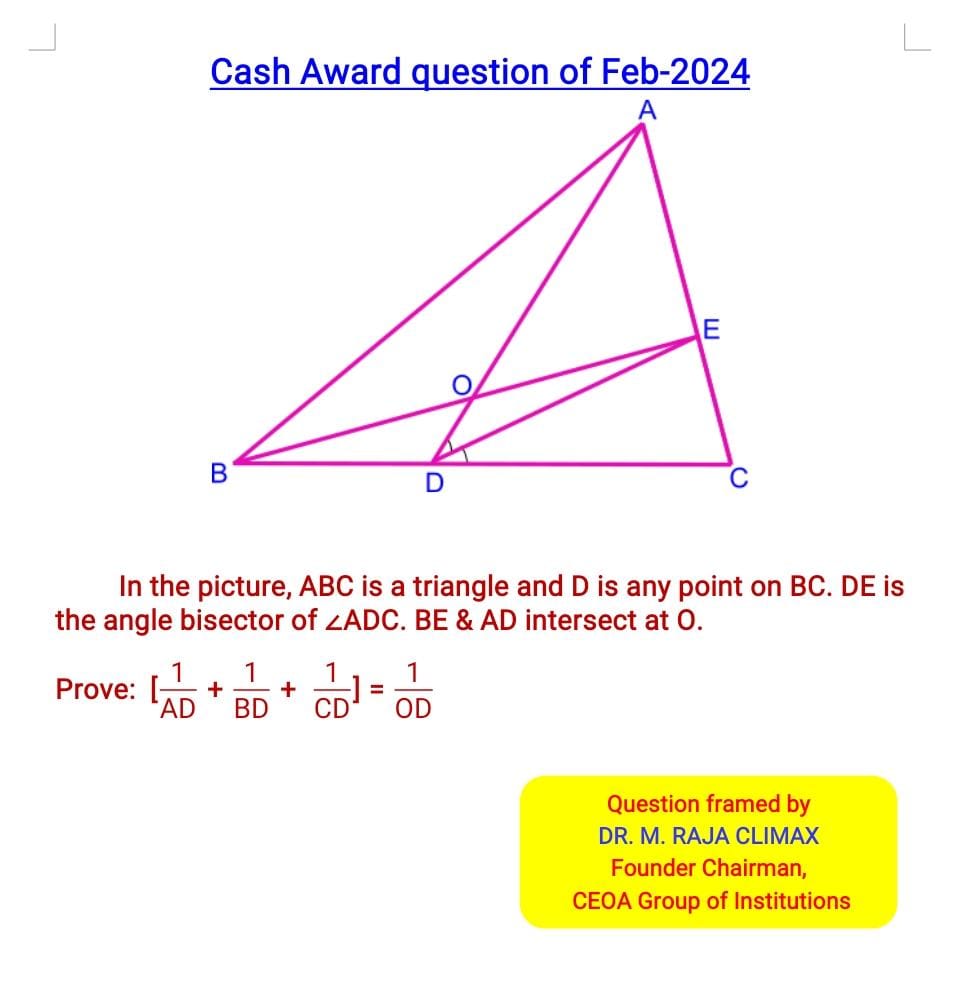
Q.21 Cash Award Qn posted on 01.01.2024
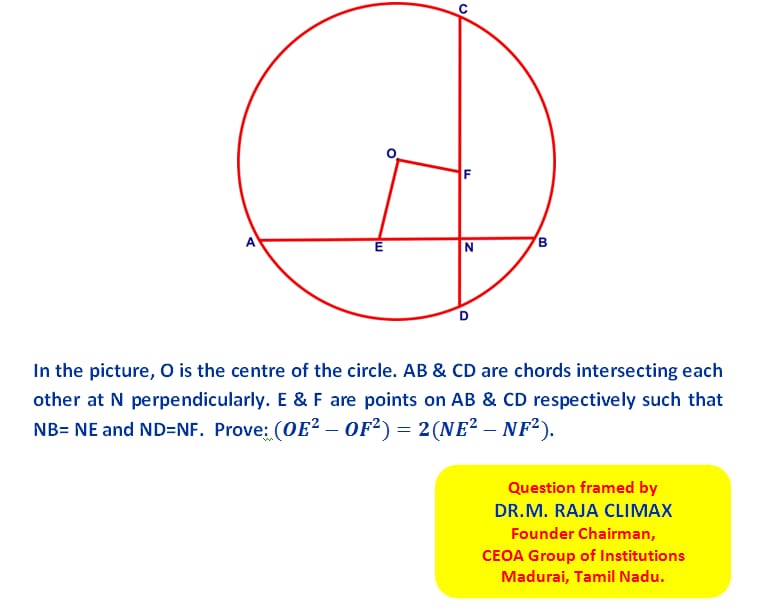
Q.20 Cash Award Math Rider posted on 01.12.2023

Q.19 Cash Award Qn posted on 01.11.2023
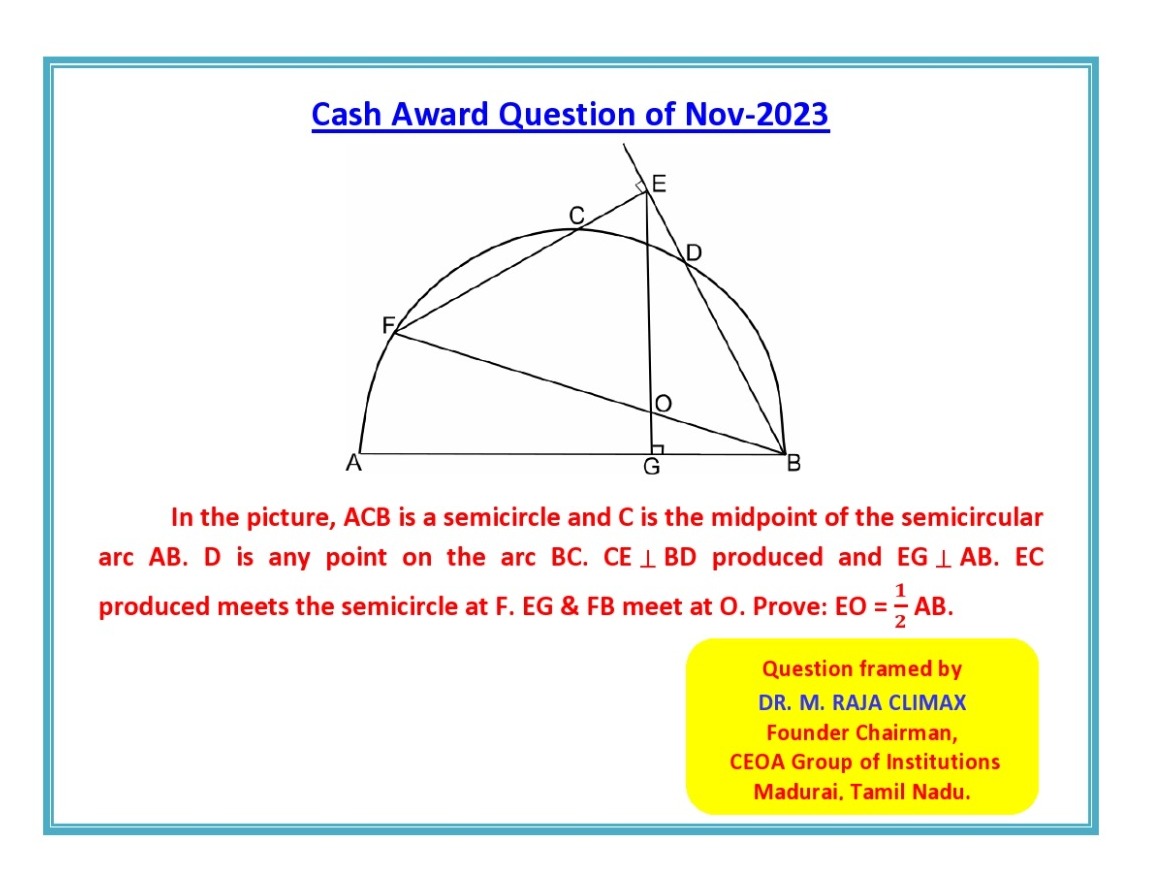
Q.18 Cash Award Qn posted on 01.10.2023
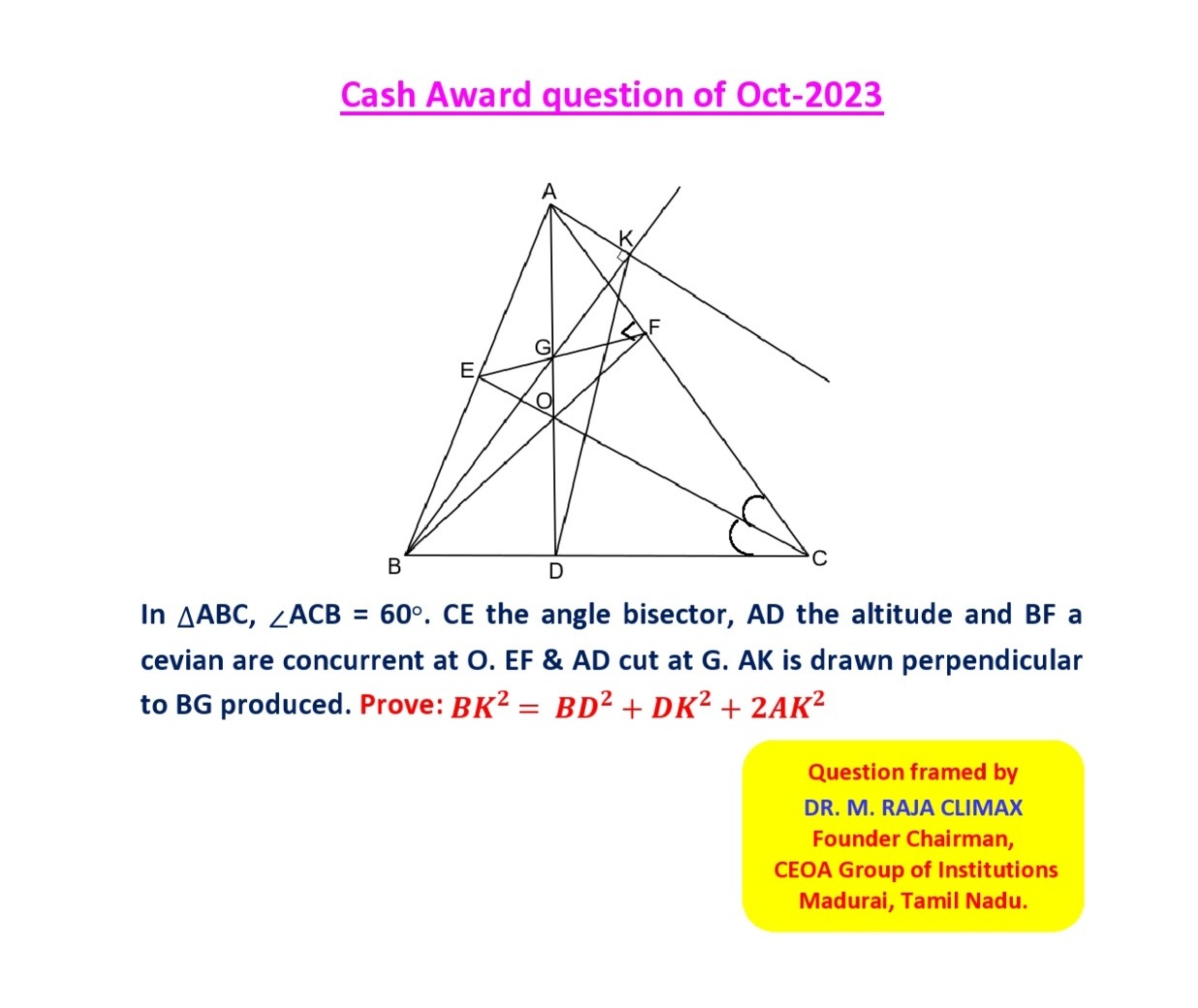
Q.17 Cash Award Qn posted on 01.09.2023
.jpg)
Q.16 Cash Award Qn posted on 01.08.2023

Q.15 Cash Award Qn posted on 01.07.2023

Q.14 Cash Award Qn posted on 01.06.2023
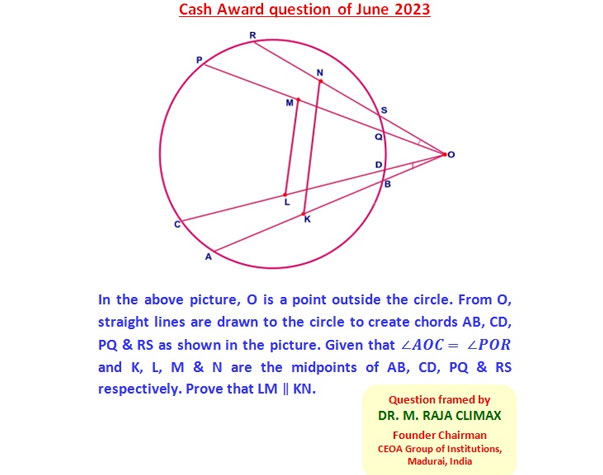
Q.13 Cash Award Qn posted on 01.05.2023
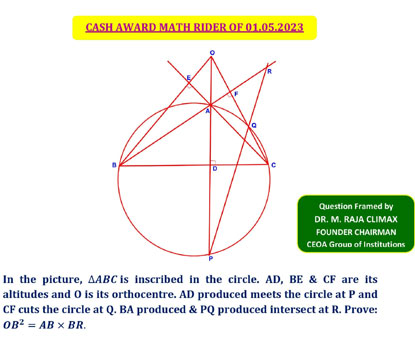
Q.12 Cash Award Qn posted on 01.04.2023
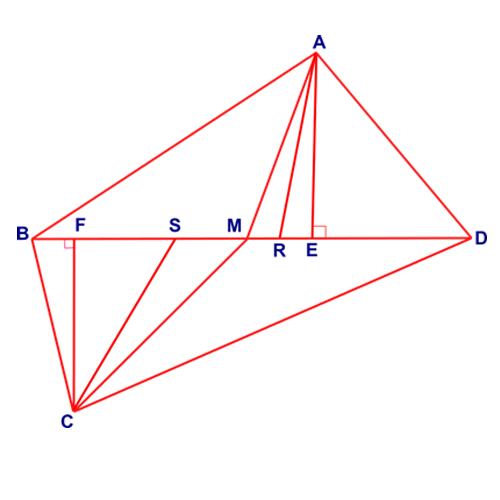
In the picture, ABCD is a cyclic quadrilateral and BD is its diagonal. AE, AR & AM are respectively the altitude, angle bisector and median of triangle ABD. Similarly, CF, CS & CM are respectively the altitude, angle bisector & median of triangle CBD. Given that AE = CF. Prove: (MS^2-MR^2) = (FS^2-ER^2).
Question created by
Dr.M.Raja Climax,
Founder Chairman, CEOA
Q.11 Cash Award Qn posted on 01.03.2023
In ∆ ABC, AB = 10 units and AD is the altitude. ∠DAC=30°. E is a point on AB produced such that BE = 2 units. ED is joined and produced to meet AC at F and DF is found to be 5 units. Prove : AF = 2FC.
Question created by
Dr.M.Raja Climax,
Founder Chairman, CEOA
Q.10 Cash Award Qn posted on 01.02.2023
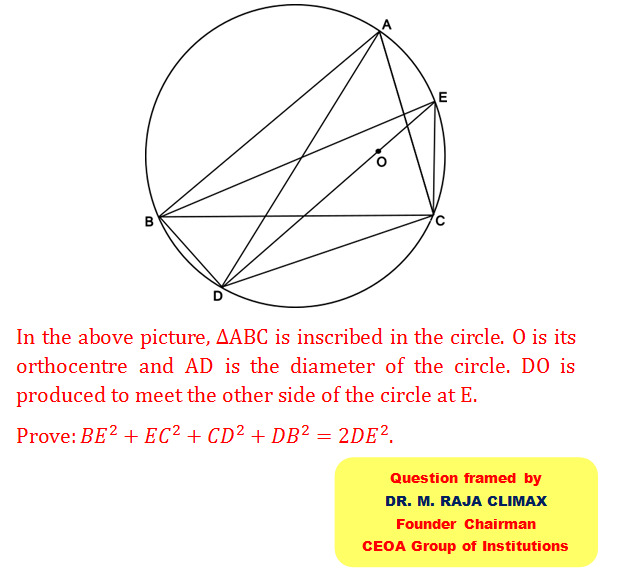
Q.9 Cash Award Qn posted on 01.01.2023

In the picture, O is the centre of the circle, AB is a chord and M is its midpoint. CD is another chord passing through M as shown in the picture and DF is the diameter. The perpendicular line drawn from C to AB meets the other side of the circle at E as shown in the picture.
Prove : The measurements of EM, DM & FC will constitute the sides of a right triangle.
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA Institutions
Q.8 Cash Award Qn posted on 01.12.2022
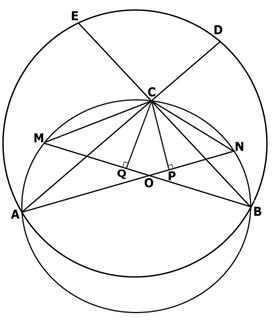
In the picture, two circles (one small and one big) intersect each other at A & B. C is any point on the major arc AB of the smaller circle. AC & BC are joined and produced to meet the bigger circle at D & E respectively. M & N are points on minor arcs AC & BC respectively of smaller circle such that CE = CM and CD = CN. AN & BM intersect at O. CP ⊥ AN and CQ ⊥ BM are drawn. Prove: OP = OQ
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA Institutions
Q.7 Cash Award Qn posted on 01.10.2022
01.10.2022 -FESTIVAL MONTH BUMPER PRIZE RIDER
ABCD is a cyclic quadrilateral where AB > AD and CB = CD. AC & BD cutat O. CE is drawn perpendicular to AB. M is the midpoint of BD. EM is joined and produced to meet AC & AD produced at N and G respectively.
Prove: AO = EM X MG/CN
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA Institutions
Q.6 Cash Award Qn posted on 01.09.2022
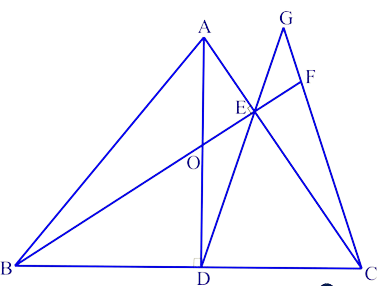
In the adjoining picture, AD & BE are altitudes of △ABC and O is the orthocentre. F is a point on BE produced such that OE = EF. DE & CF meet at G. Prove: BC/GC = FC/DC
Question created by
Dr.M.Raja Climax Founder Chairman, CEOA Institutions
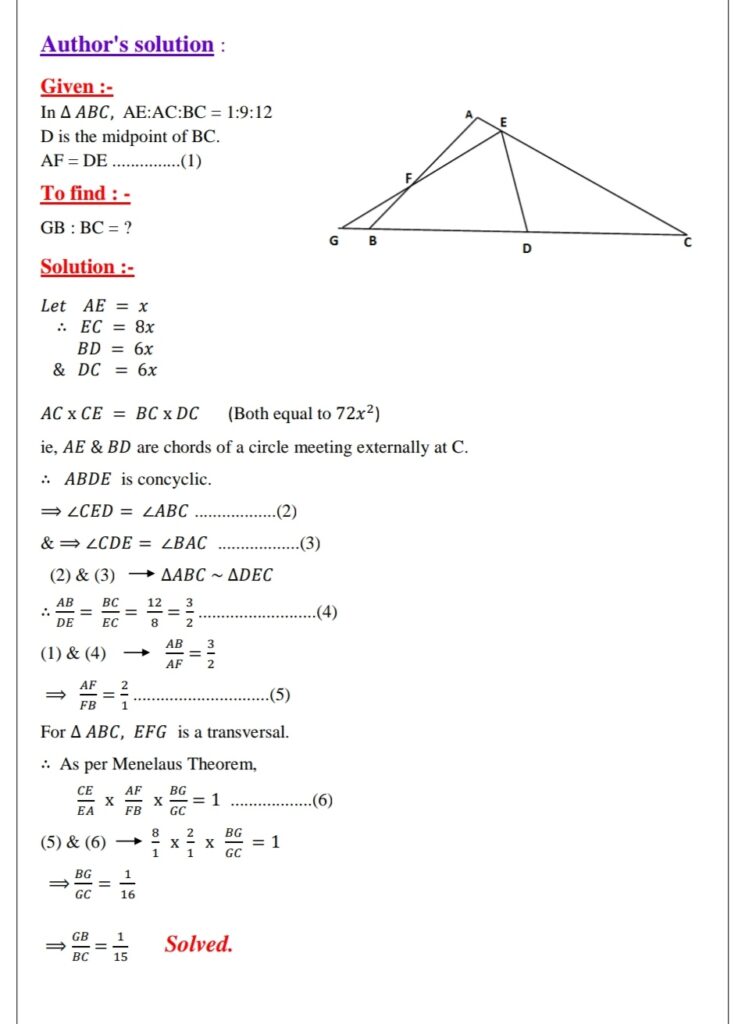
Q.5 Cash Award Qn posted on 01.08.2022
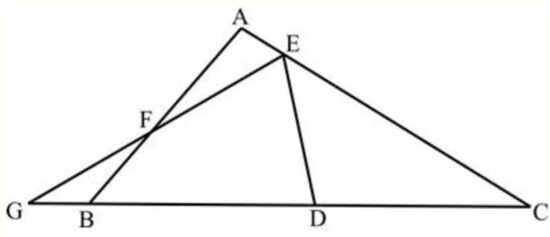
In the adjoining figure, AE: AC: BC= 1:9: 12, D is the mid-point of BC and AF=ED.
Find GB : BC. A
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA Institutions
Q.4 Cash Award Qn posted on 01.07.2022
For triangle ABC, AD is a median with AD = BC and Ois the circumcentre. OE is perpendicular to AD. CE is joined and produced to meet AB at F.
Prove: CE/EF = 11/5.
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA Institutions
Q.3 Cash Award Qn posted on 01.06.2022
ABCD is a quadrilateral with BC = CD and AB > AD. The diagonal AC is also the internal bisector of ZBAD. CE is drawn perpendicular to AB. M is the midpoint of BD. EM is joined and produced to meet CD at F.
Prove that BM = CExFM / FC
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA Institutions
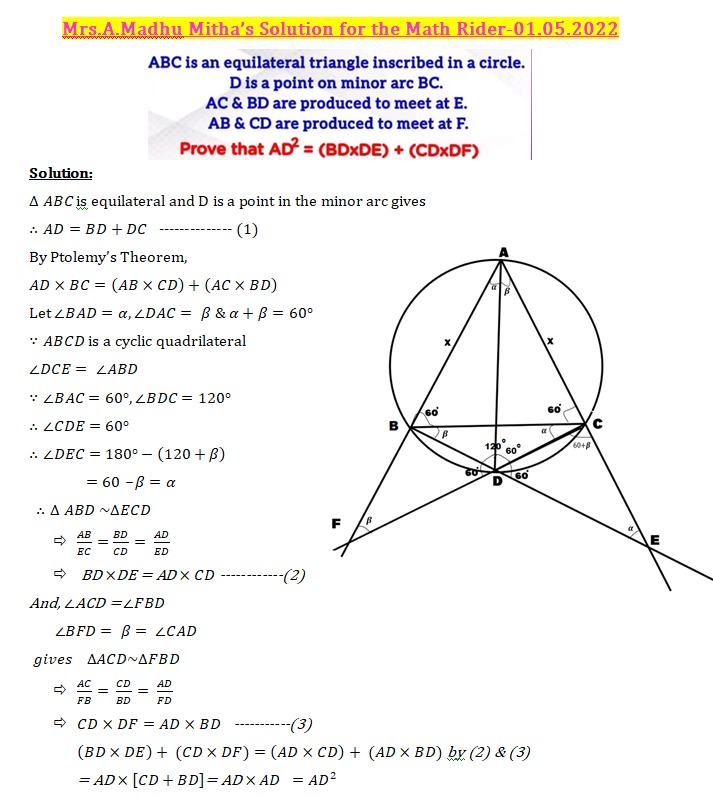
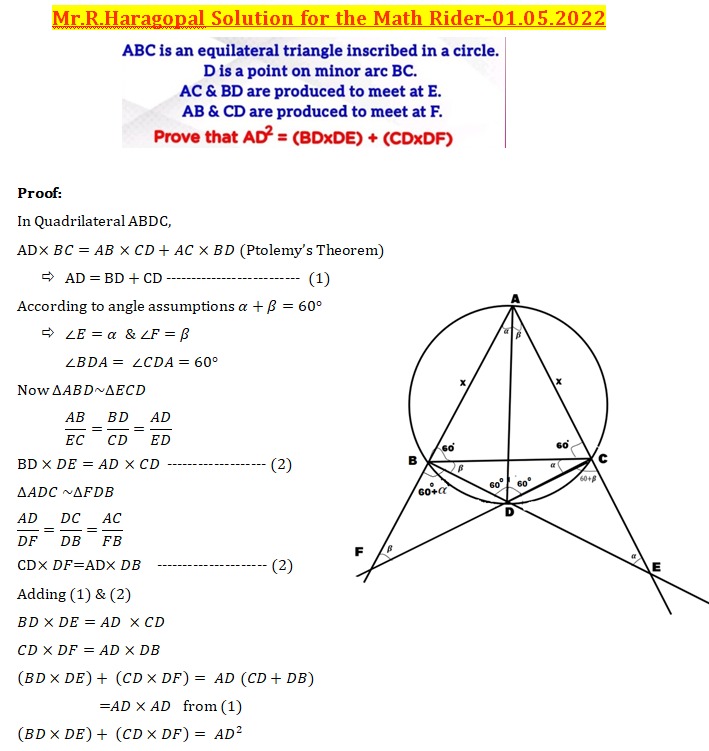
Q.2 Cash Award Qn posted on 01.05.2022
ABC is an equilateral triangle ioeribed ina eircle.Disa point on minor arc BC.
AC & BD are produced to meet at E. AB & CD are produced to meet at F.
Prove that AD2 = (BD*DE) + (CD*DF)
Q.1 Cash Award Qn posted on 31.03.2022
In triangle ABC, BD is a median with G, the Centroid on it. M is the midpoint of GD. P is a point on AD such that AP = 2PD. AM is joined and produced to meet GC at N. PN is joined and produced to meet BC at Land ALis joined to cut GM at O. prove that BO = 40D.
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA