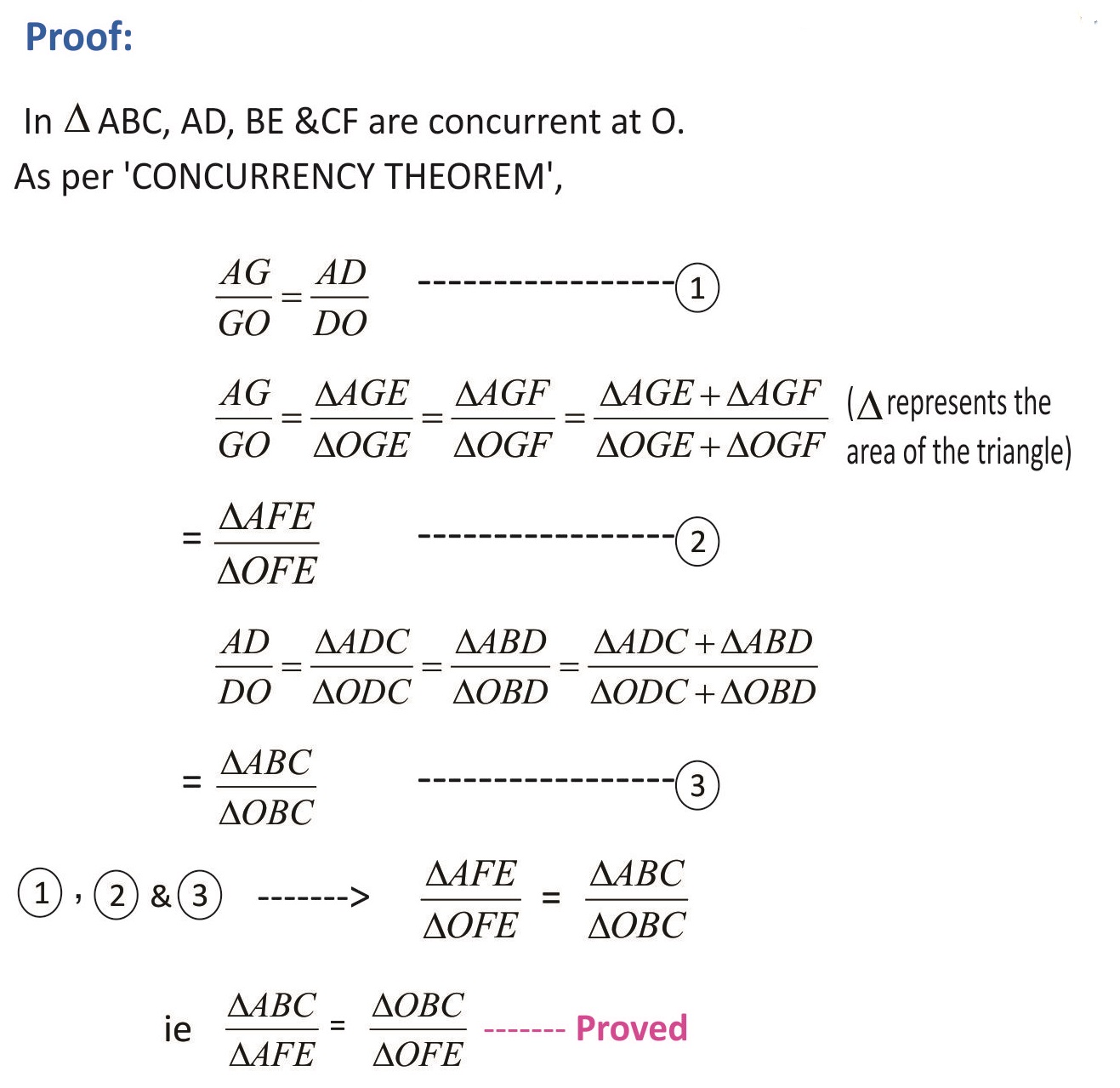
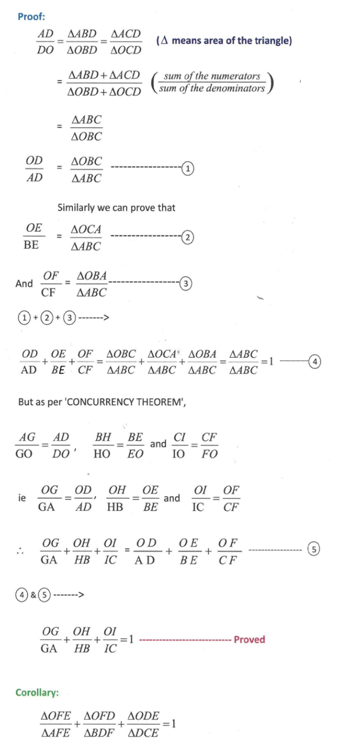
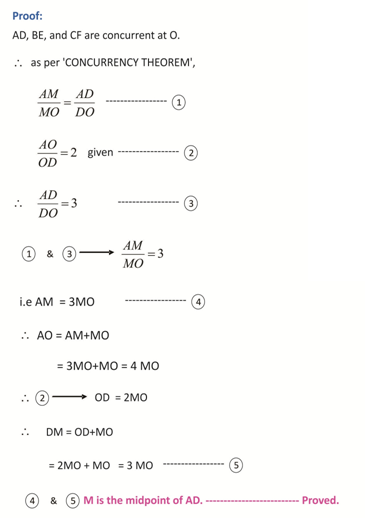
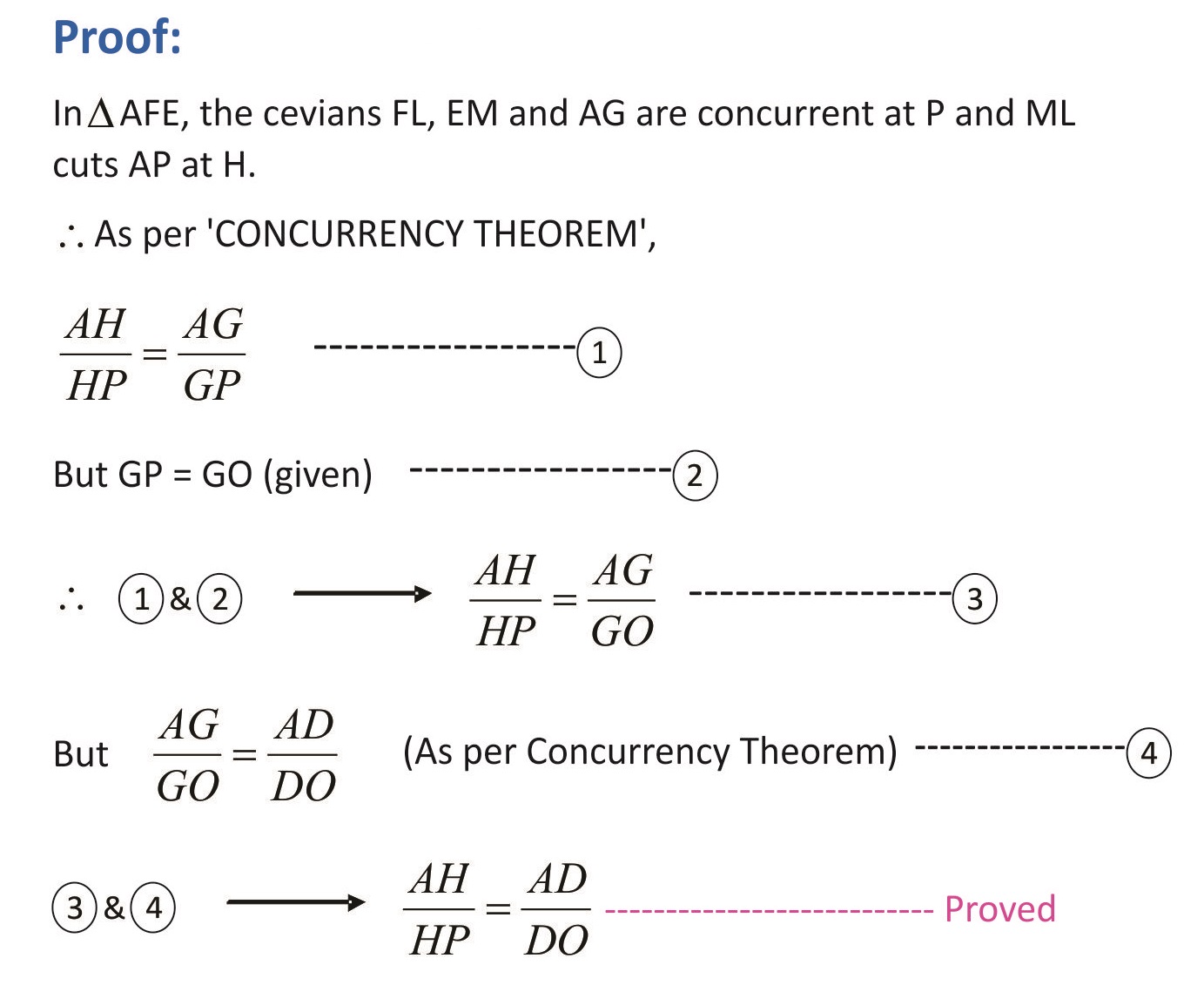
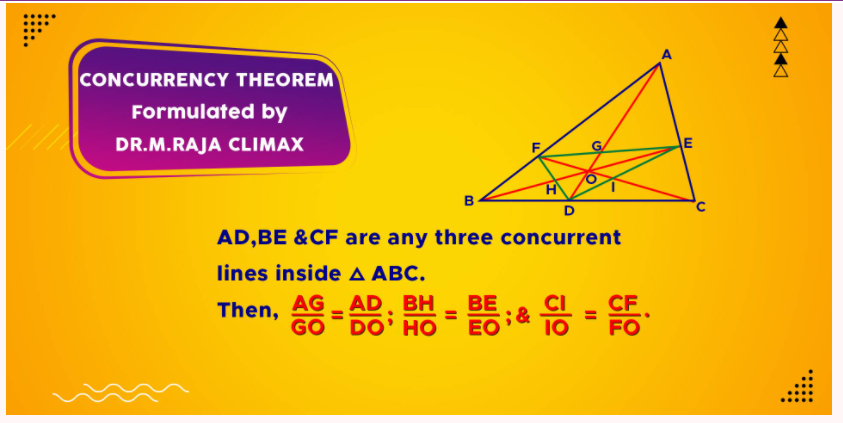
Warning: session_start(): Session cannot be started after headers have already been sent in /home/mxcuukze9tzv/public_html/maxgeometricmaths.co.in/wp-includes/header.php on line 1

The Concurrency Theorem brings out a useful result for the concurrent lines drawn inside a triangle. The said result is a further development from the Menelaus theorem. The Concurrency Theorem employs Menelaus theorem to prove the said interesting result. This theorem has been named as the CONCURRENCY THEOREM for the simple reason that it springs out from the concurrent lines drawn from the three vertices of a triangle. The concurrent lines drawn from the vertices are geometrically known as ‘cevians’. Though this result (the Concurrency Theorem) is already in existence in the arena of Geometry as a simple feature of a quadrangle with a corollarical significance, the same is presented here in a new form and projected with a new proof. Moreover, based on the concurrency theorem 25 beautiful riders have been developed & given here.

Concurrency Theorem

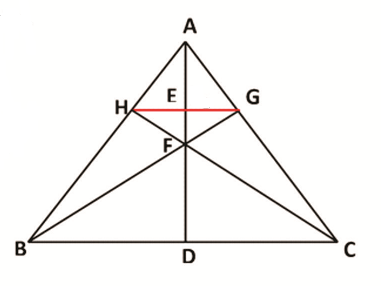
Converse of Concurrency Theorem

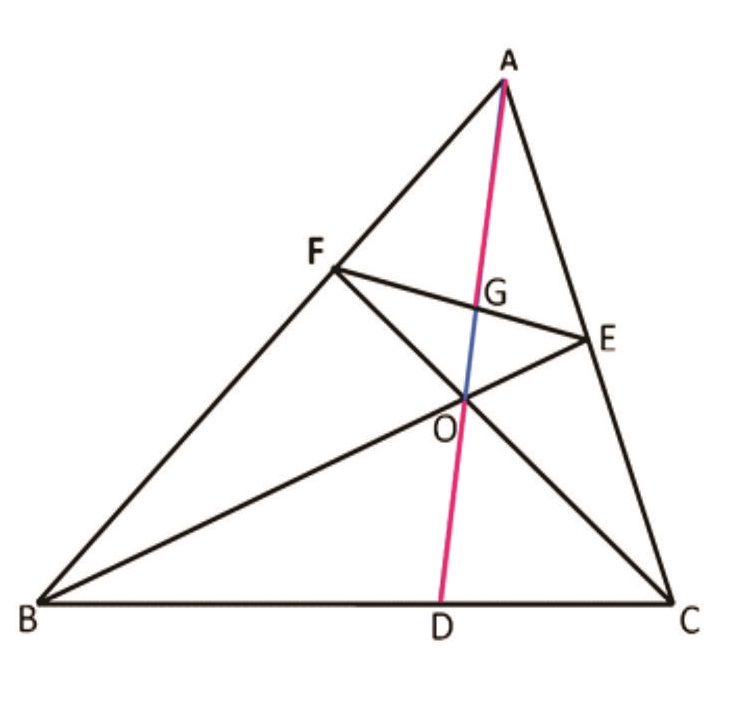
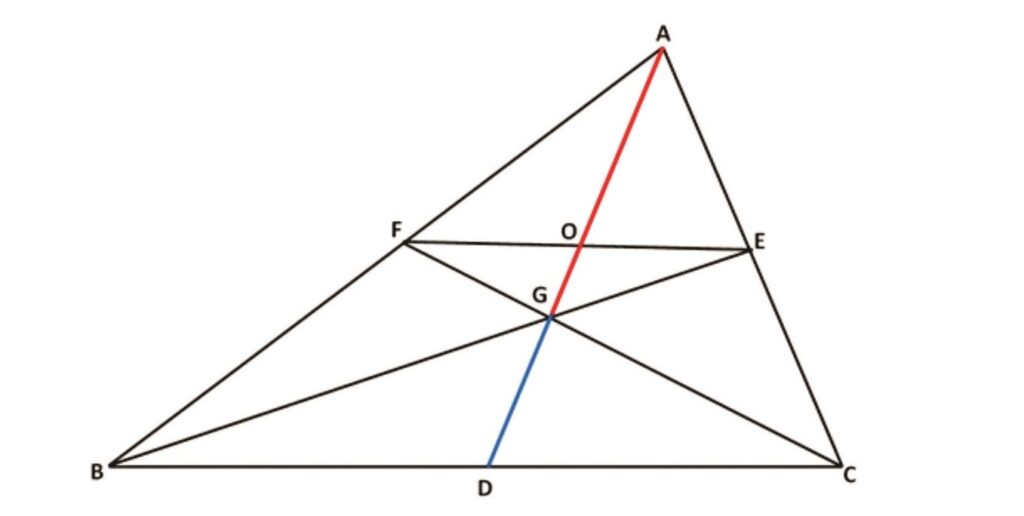
Rider : 1

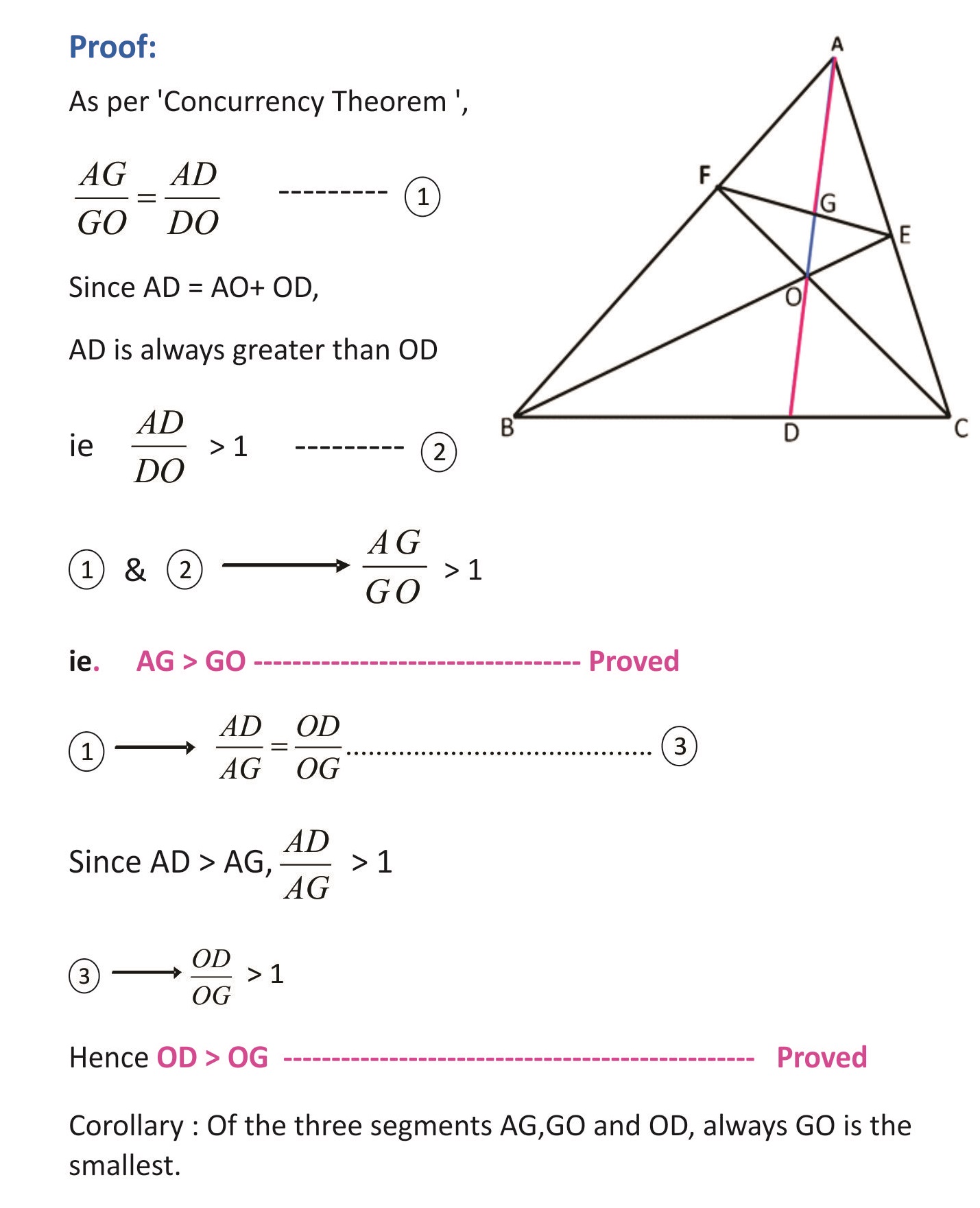
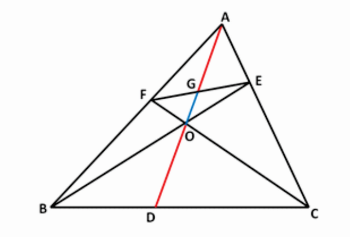
In Δ ABC, AD, BE and CF are cevians concurrent at O meeting BC, CA and AB at D, E and F respectively. EF and AD cuts at G. Prove that AG and OD are always greater than GO.

Rider : 2

Using ‘Concurrency Theorem’, prove that the centroid of a triangle divides its medians in the ratio of 2 : 1.

Rider : 3

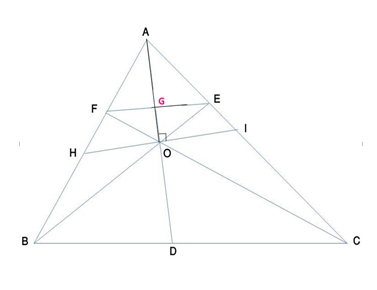
In ΔABC, AD is the bisector of angle A meeting BC at D. O is the mid-point of AD. BO and CO are produced to meet AC and AB at E and F respectively and EF cuts AD at G. The line drawn perpendicular to AD at O meets AB and AC respectively at H and I. Prove that G is the centroid of triangle AHI.

Rider : 4

In ΔABC, AD is any straight line (cevian) drawn from vertex A to meet BC at D. O is the mid-point of AD. BO and CO are produced to meet AC and AB at F and E respectively. EF cuts AO at G. Prove that OG / AD = 1/6

Rider : 5

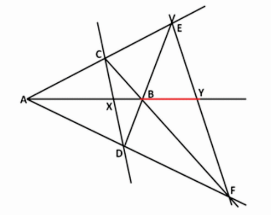
AB is a straight line. X is a point on AB lying between A and B and dividing AB in a particular ratio. Find out the point Y on AB produced which divides AB externally in the same ratio ie. such that AX / XB = AY / YB

AB is the given line. Xis lying in between A and B. To find out Y, the point on AB Produced (which divides AB externally in the same ratio as X does internally), let us follow the following method.

Draw any line through X and mark the points C and D on the same line on either side of X as shown in the figure. Join AC and AD and produce them. Join DB and CB and produce them to cut AC produced and AD produced at E and F respectively. Join EF to cut AB produced at Y. Now Y is the required point.

‘The above exercise can be repeated by drawing fresh lines through X, A,etc, in the same picture. It can be seen that the same point Y will be resulted as shown in the picture below. (The new lines are shown inblue color.)

Rider : 6

In Δ ABC, M & N are points on AB & AC respectively such that MN is parallel to BC. X and Y are points on BC and the lines AX & AY (drawn to meet BC at X and Y) intersect MN at D & E respectively. The concurrent lines drawn from B & C through D meet AC & AB at G & F respectively and FG intersect AX at H. The concurrent lines drawn from B & C through E cuts AC & AB at J & I respectively and I J cuts AY at K. Prove that HK is parallel to BC

Rider : 7

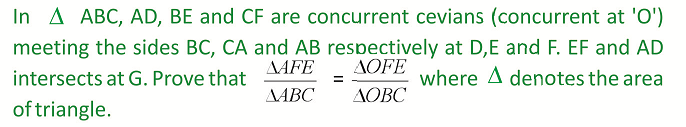
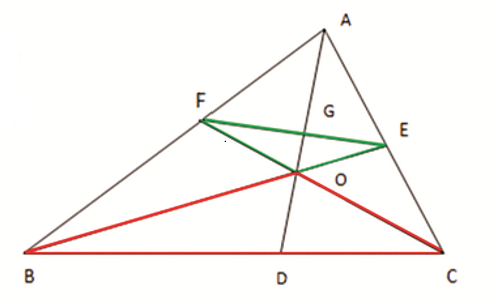
Rider : 8

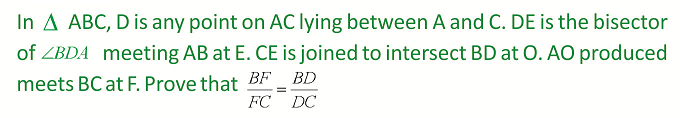
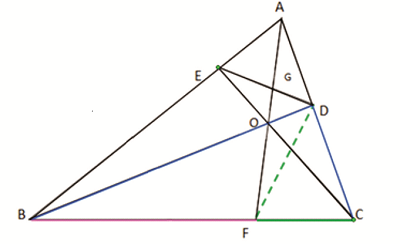
Rider : 9

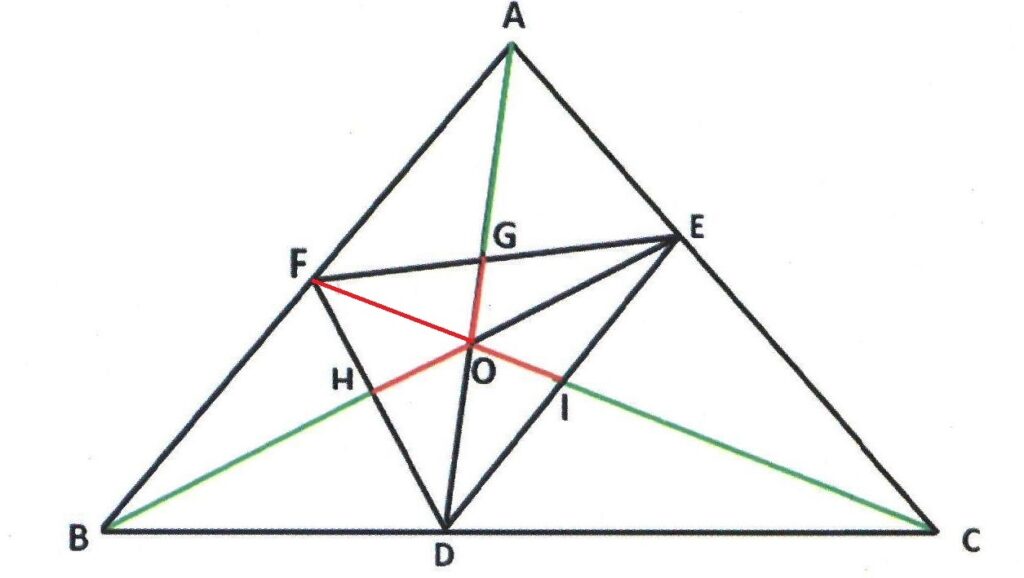
Rider : 10

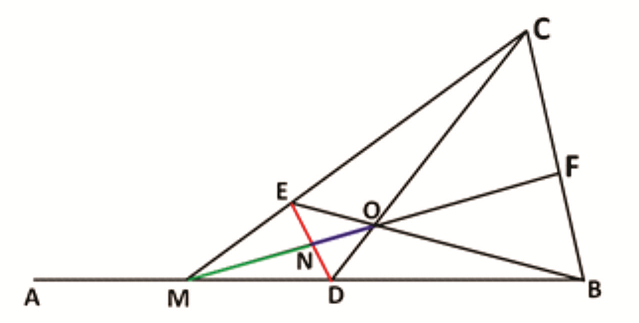
Rider : 11

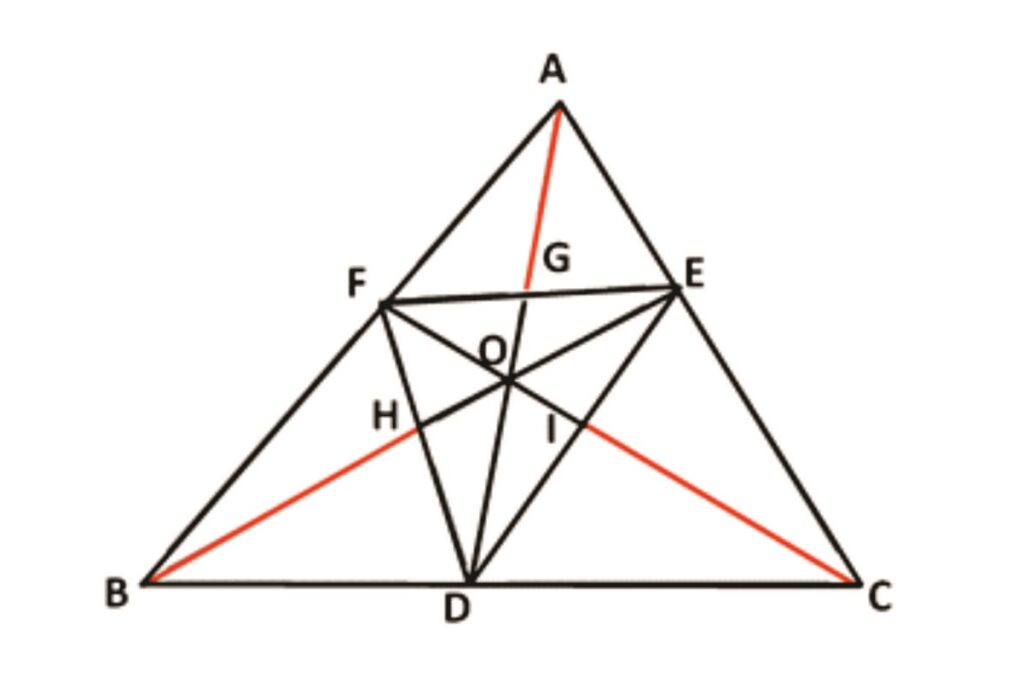
Rider : 12

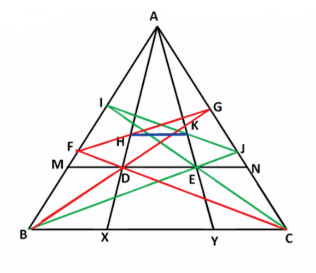
In Δ ABC, AD, BE and CF are Cevians concurrent at ‘O’. FE is produced to meet BC produced at G. AD is produced and H is a point on AD produced. BE is produced to meet HC produced at I. BH and FC are produced to meet at J. Prove that J, G and I are collinear.

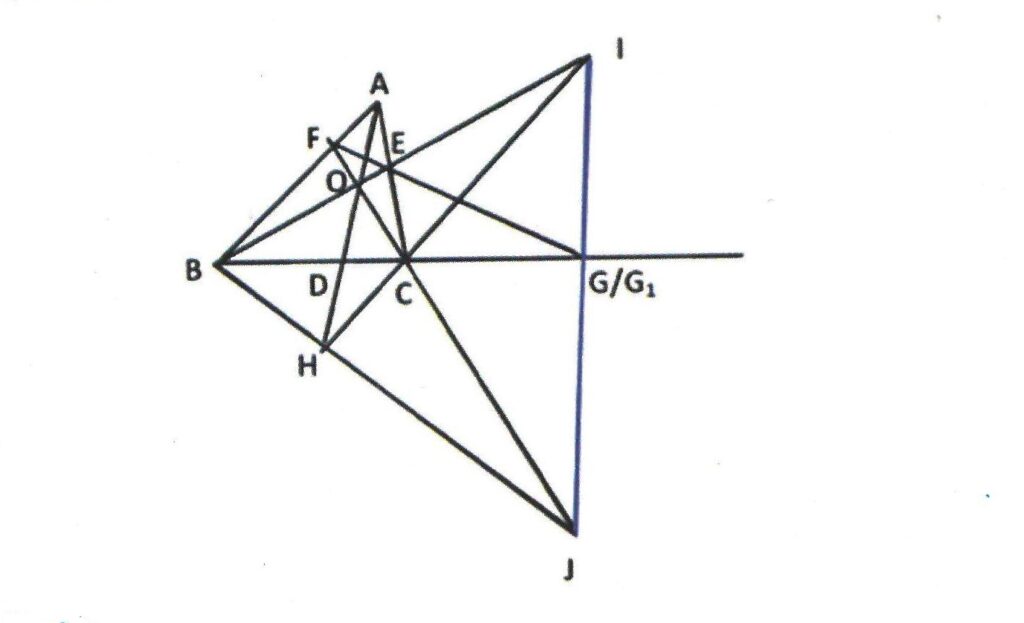
Rider : 13

The above rider proves this mid-point property for any cevian (not only median but also all Cevians). ie For any cevian, if concurrent lines (Cevians) are drawn from the other two vertices through its point dividing itself in the ratio of 2:1, then, the line joining the base points of those two other Cevians will cut the first cevian at its mid point. The locus of the mid-points of all such Cevians of a particular vertex will be a parallel line passing through the mid-points of the two sides forming the vertex.

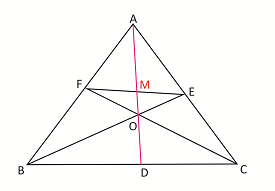
Rider : 14

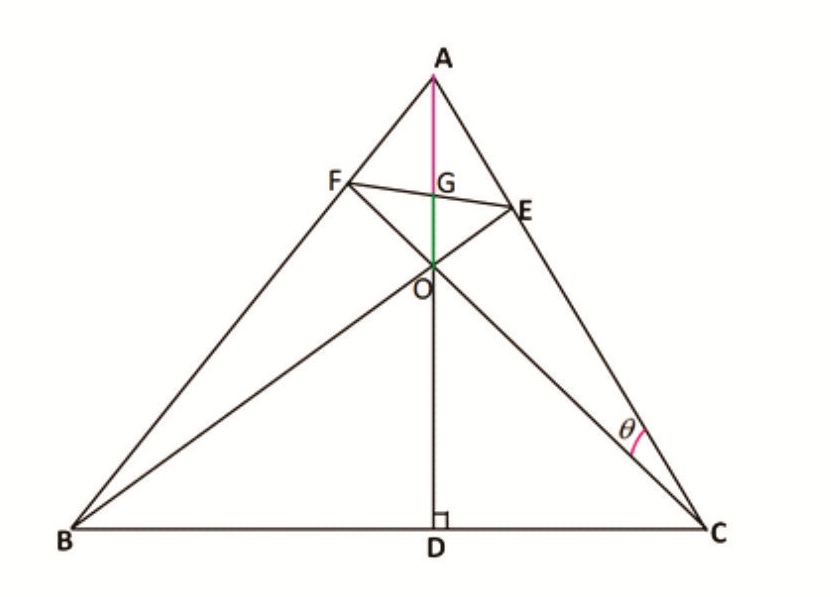
Rider : 15

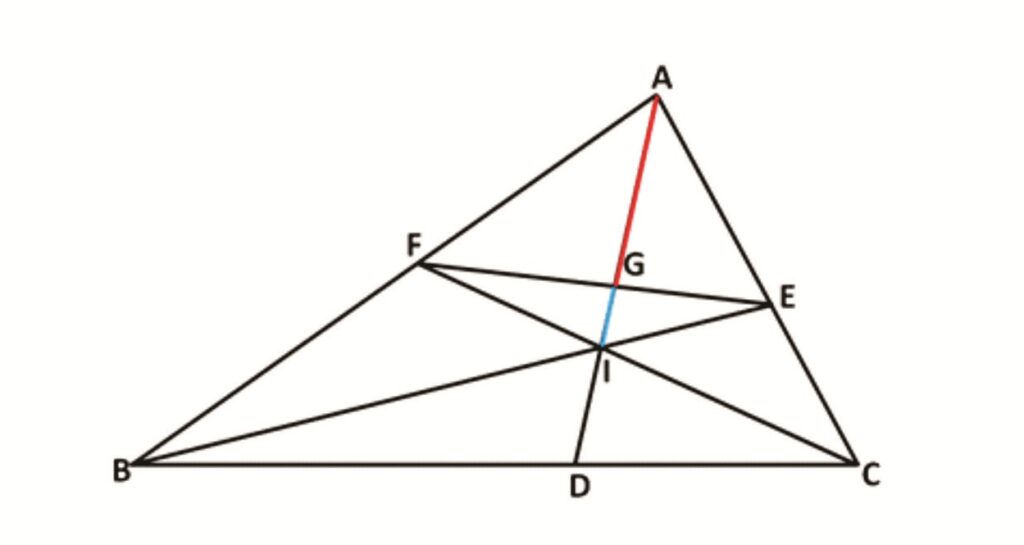
Rider : 16

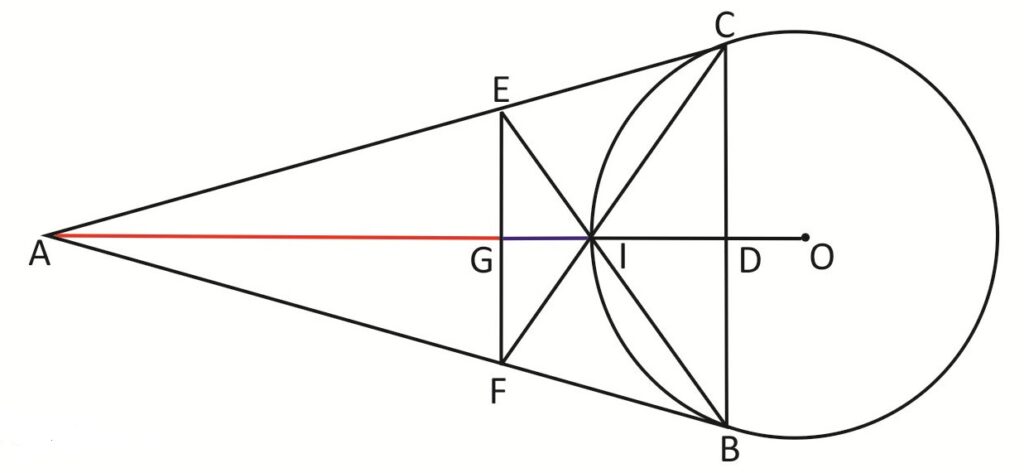
Rider : 17

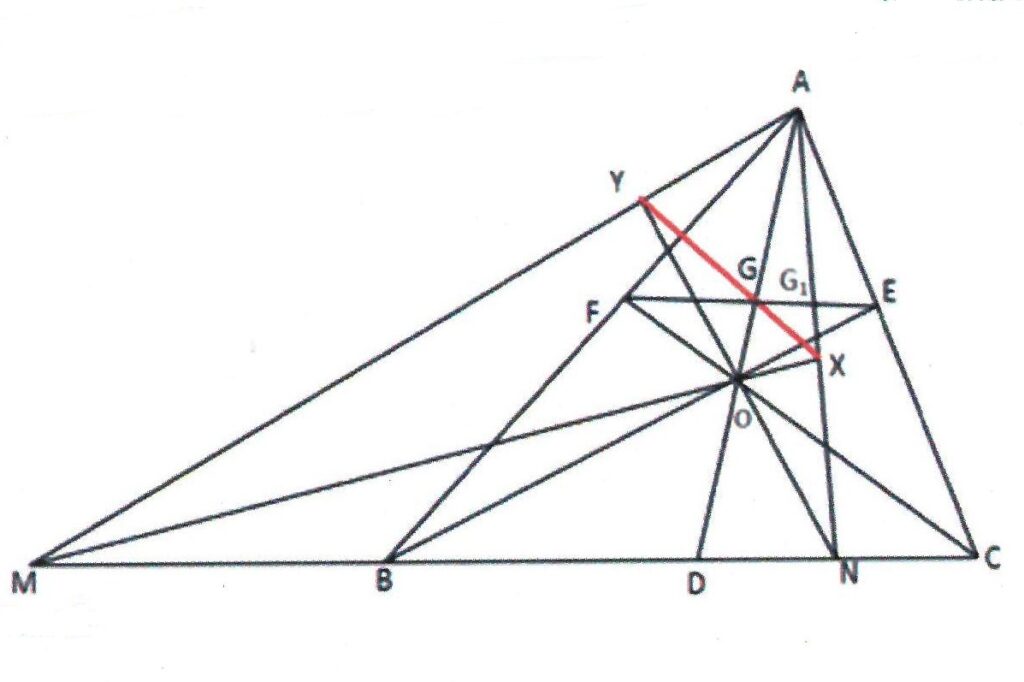
In Δ ABC, AD, BE and CF are Cevians concurrent at O meeting BC, CA and AB at D, E and F respectively. FE and AO cut at G. M and N are any two points on BC. AM and AN are joined to make Δ AMN. MO and NO are joined and produced to meet AN and AM at X and Y respectively. Prove that X, G and Y are collinear.

Rider : 18

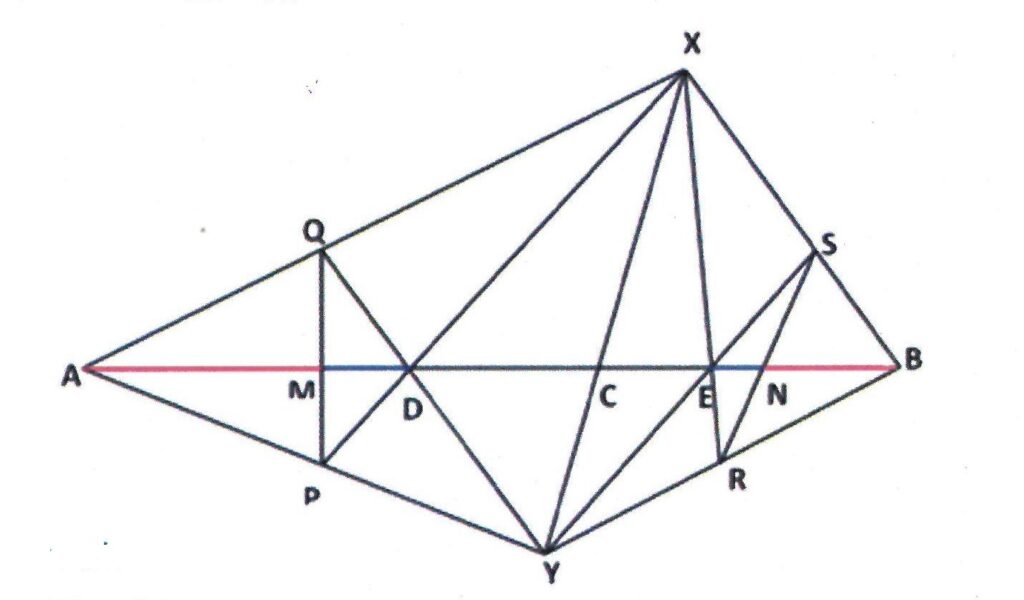
Rider : 19

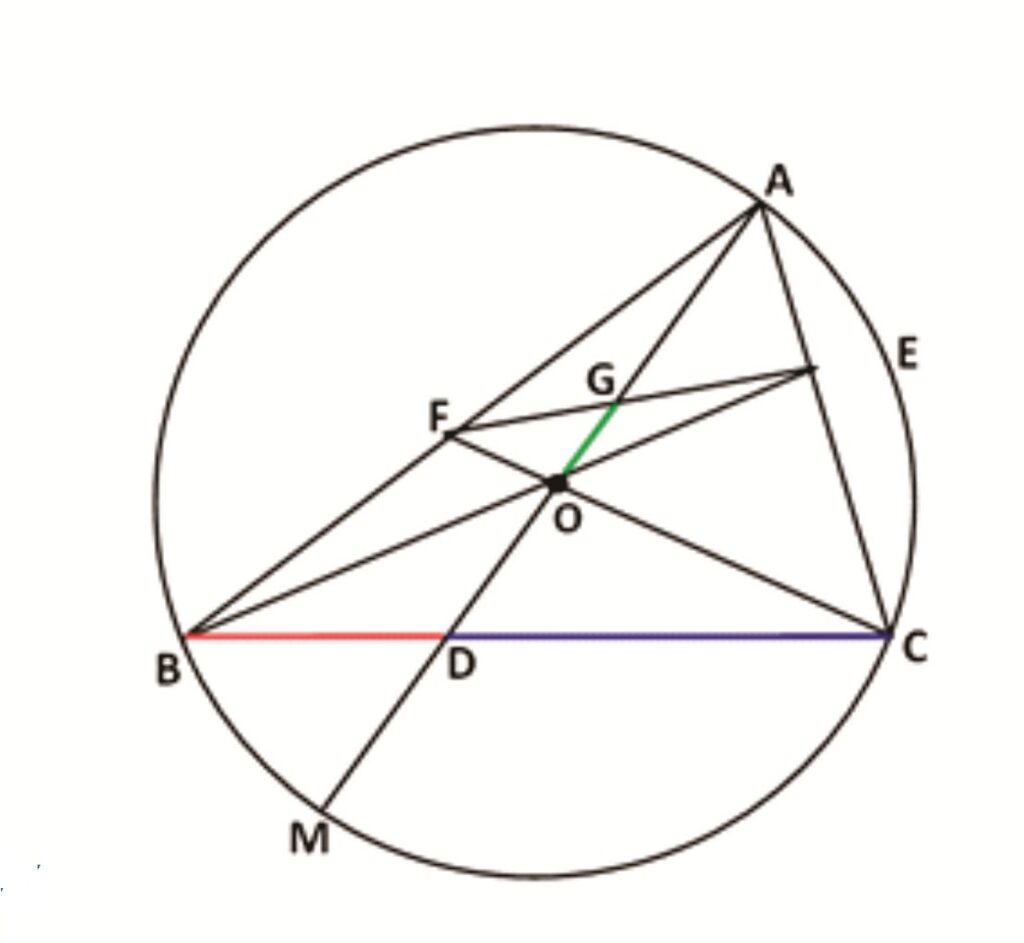
In a circle with centre at O, AOM is a diameter. D is the midpoint of OM and BC is a chord passing through D. AB and AC are joined to make ABC. Cevians are drawn from B and C through O to meet AC and AB at E and F respectively. FE and AO cut at G. Prove that BD x DC = 12 OG

Rider : 20

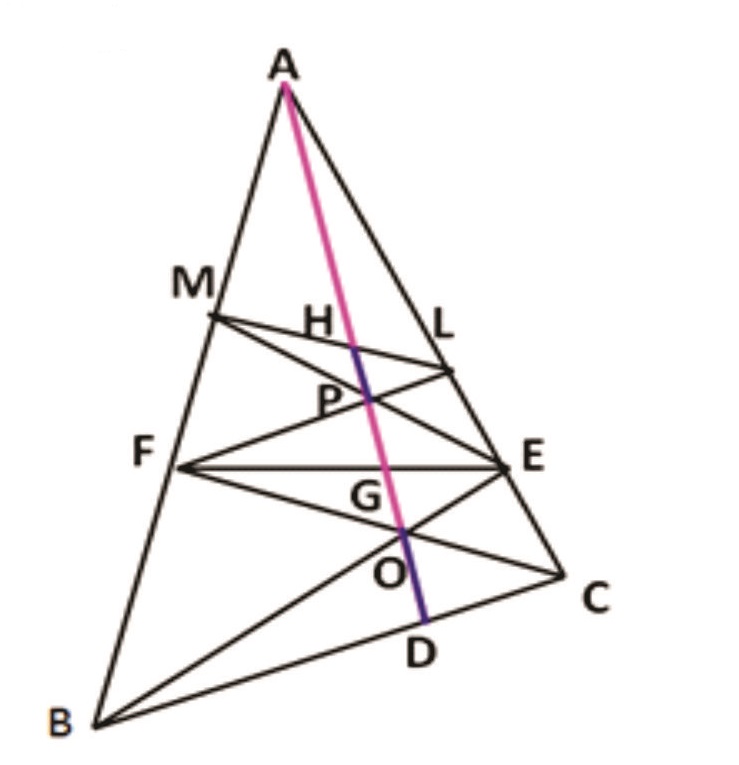
Rider : 21(a)

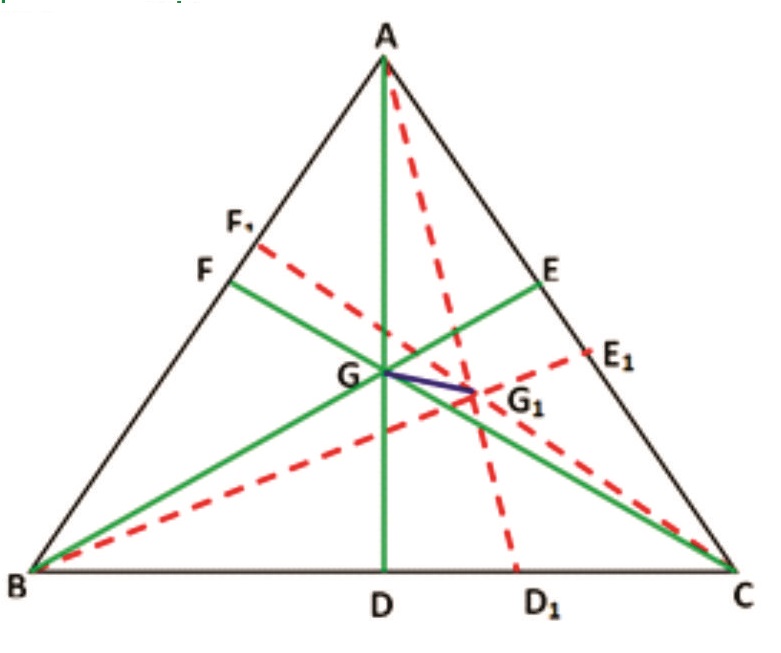
Prove that the centroid of a triangle is the one and only point dividing its cevians in the ratio of 2:1.

Rider : 21(b)

AB is a straight line segment with midpoint M. AX and BY are straight lines drawn through A and B cutting each other at O. G and H are points on AO and BO respectively such that OA = 4OG and OB = 4OH. MG and MH are joined and produced to cut BY and AX at D and E respectively. AD and BE meet at C. Prove that O is the centroid of the Δ ABC.

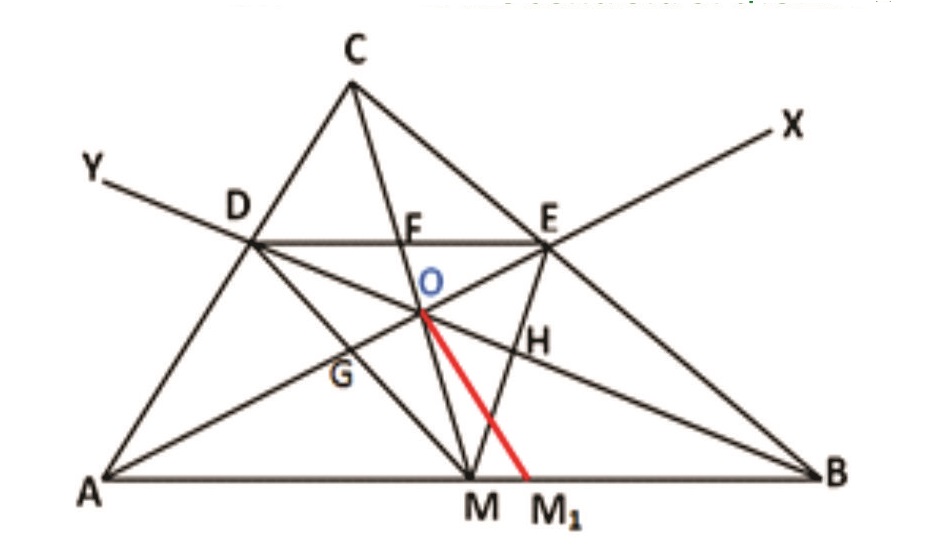
Rider : 22

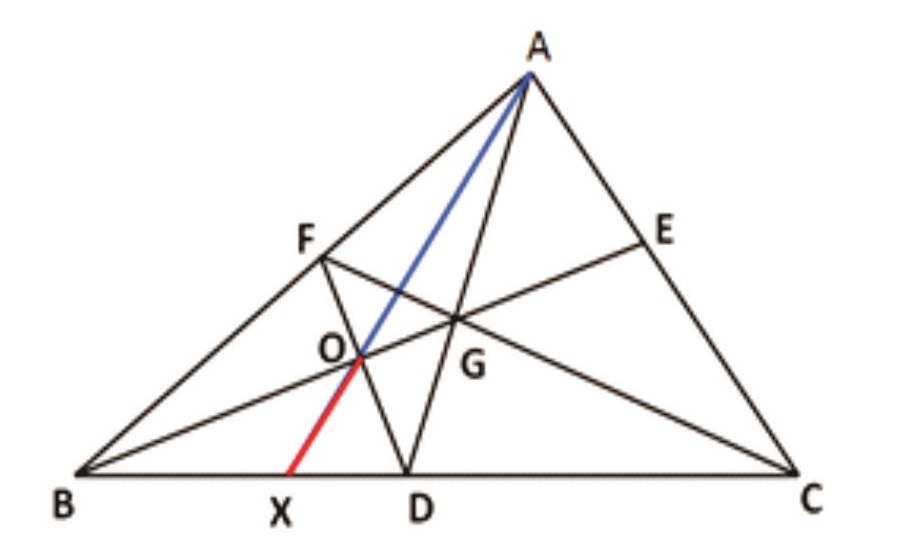
AD, BE and CF are the medians of the Δ ABC concurrent at G, the centroid. DF cuts BE at O. AO produced meets BC at X. Prove that AX = 4OX.

Rider : 23

AD, BE and CF are cevians of ΔABC concurrent at O. FE cuts AD at G. A line is drawn through G parallel to BE to cut AC at P and DE produced at Q. AQ and FE are produced to meet at R. DR is joined to cut AC at S. Prove that DSR is parallel to GQ. Hence, deduce that S is the midpoint of DR.

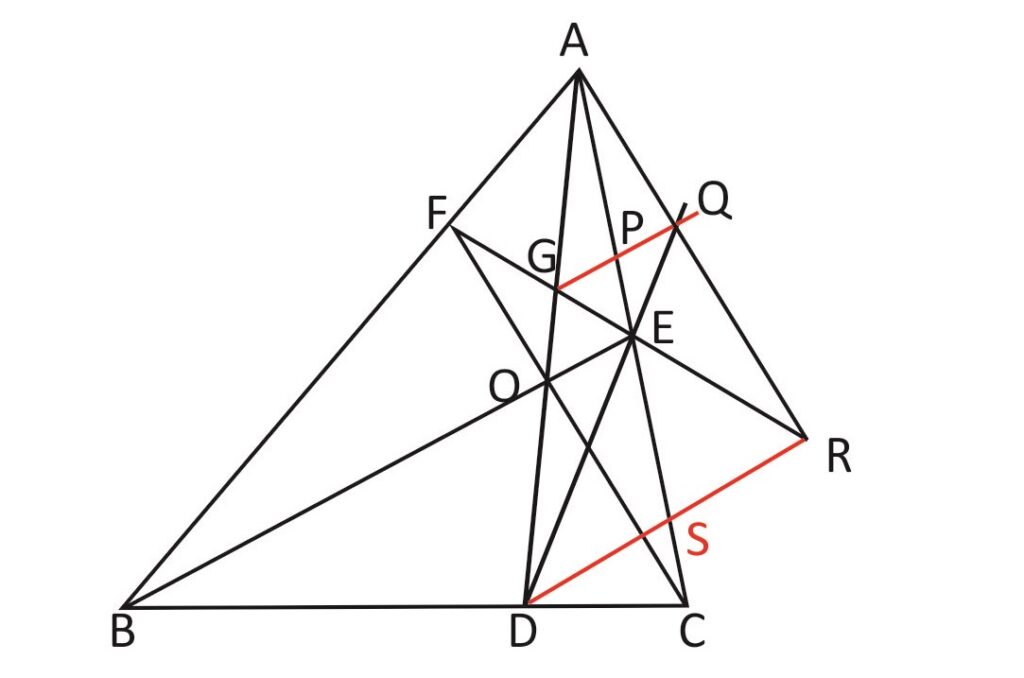
Rider : 24

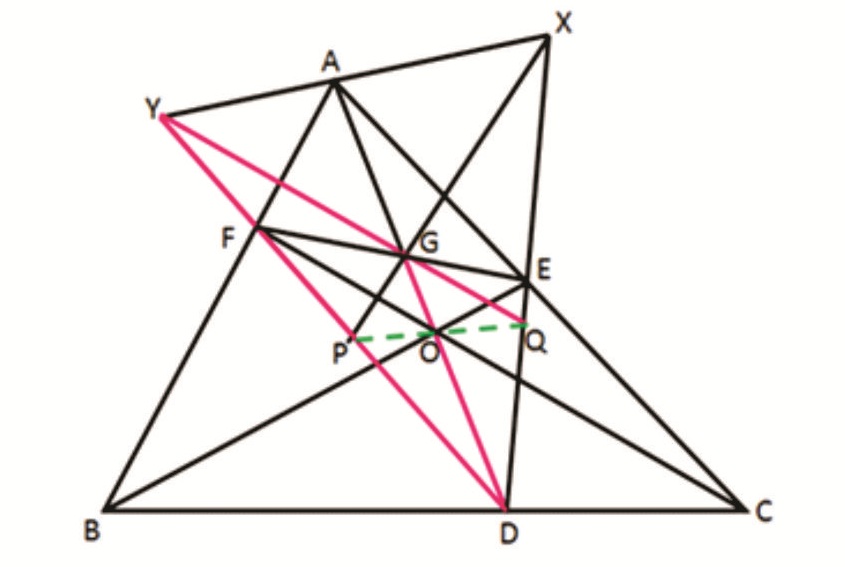
Rider : 25

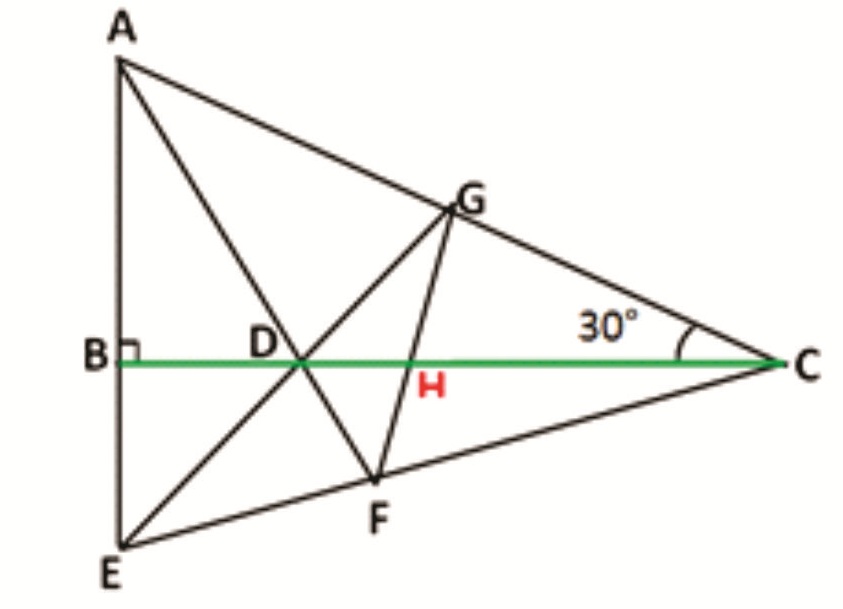
ΔABC is a right angled triangle with right angle at B and 30° at C. AD is the bisector of meeting BC at D. E is a point on AB produced. EC cuts AD produced at F. ED produced meets AC at G and GF and BC cut at H. Prove that H is the midpoint of BC.

Processing!