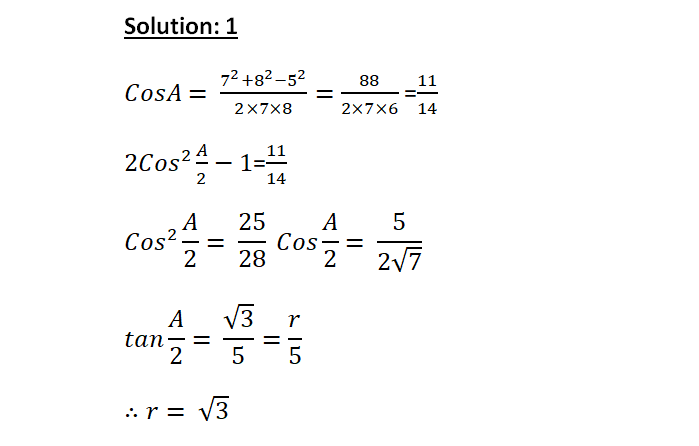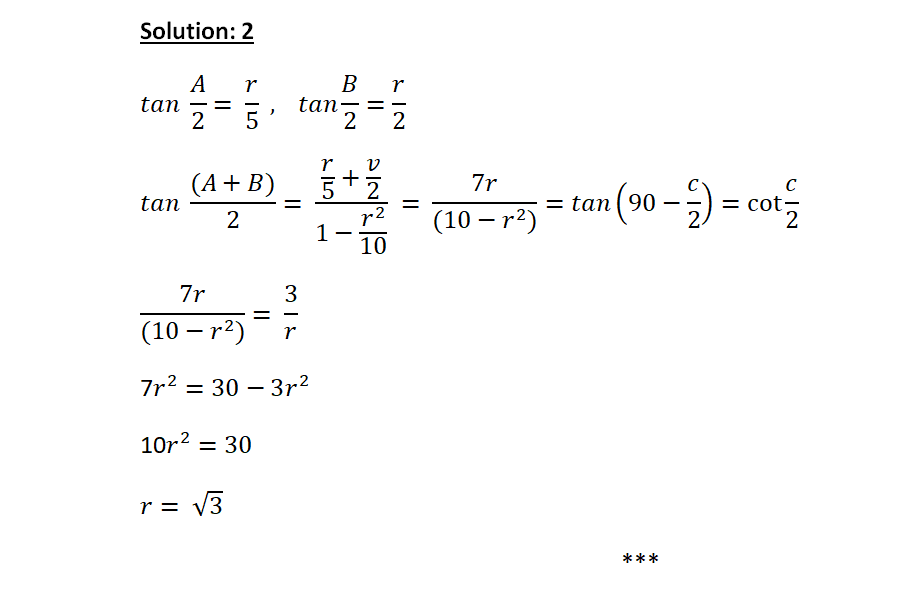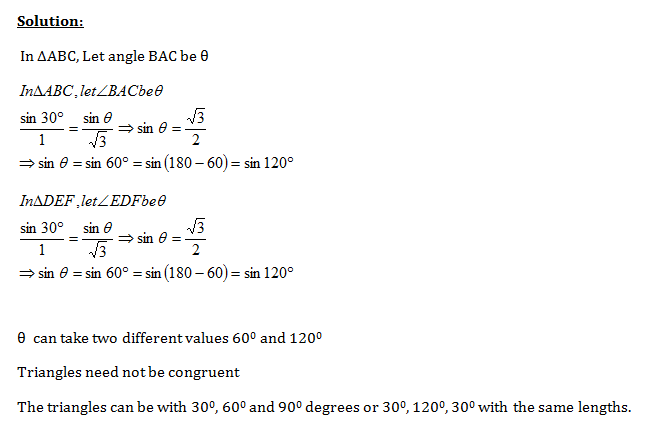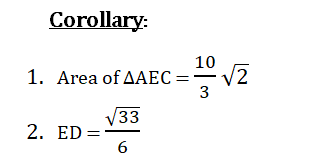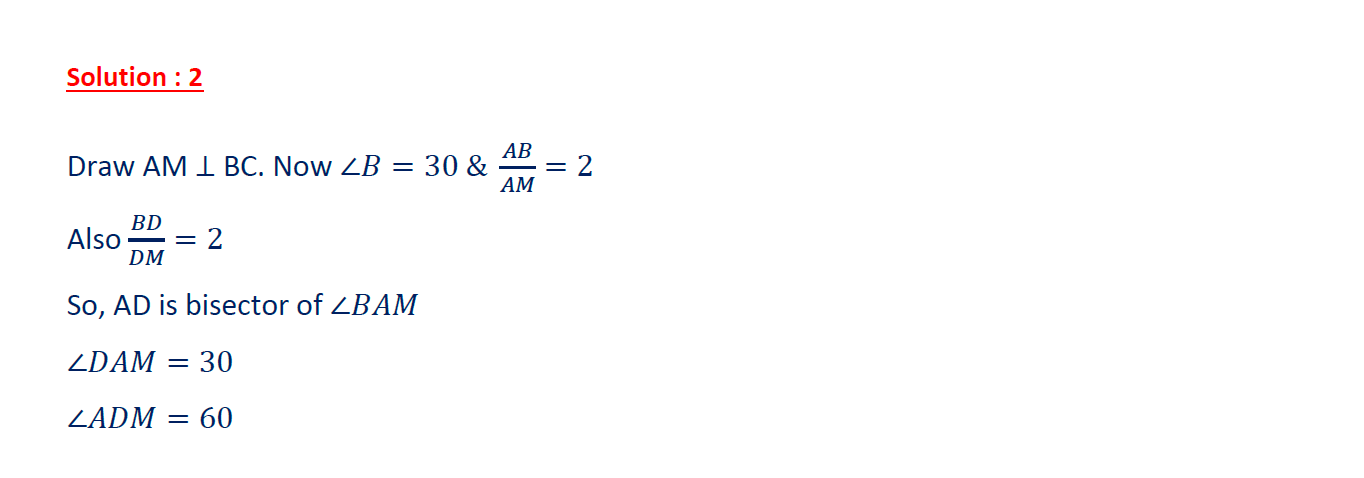Congruent Triangles
Two triangles are congruent if their corresponding sides and their corresponding interior angles are equal.
(i.e., Triangles are of same shape & size)
Notation for Congruency:
- 1. Δ ABC ‘is congruent to’ Δ DEF is notated as Δ ABC ≅ Δ DEF.
- 2. Corresponding Parts of Congruent Triangles are Congruent
CONGRUENT TRIANGLES POSTULATES
Two triangles are congruent if it satisfies anyone of the following postulates:
- 1. SSS Postulate
- 2. SAS Postulate
- 3. ASA Postulate
- 4. AAS Postulate
- 5. RHS Postulate
Postulate 1
CONGRUENT TRIANGLES
SSS Theorem (Side-Side-Side)
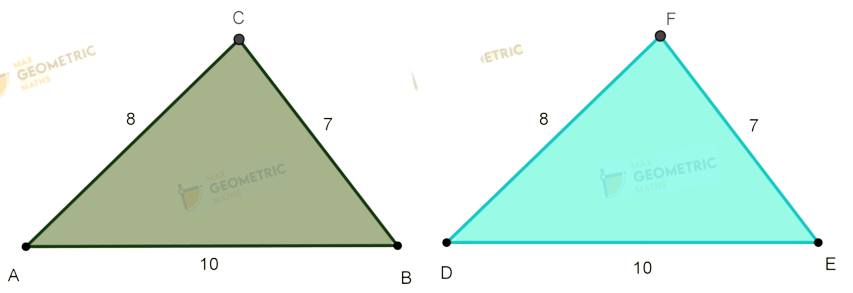
If three sides of one triangle are equal to the corresponding sides of the other triangle, then the triangles are congruent
You can observe that,
In ΔABC ΔDEF,
AB = DE = 10
AC = DF = 8
BC = EF = 7
The corresponding sides of the triangles are equal.
Hence ΔABC ≅ ΔDEF
Postulate 2
CONGRUENT TRIANGLES
SAS Theorem (Side-Angle--Side)
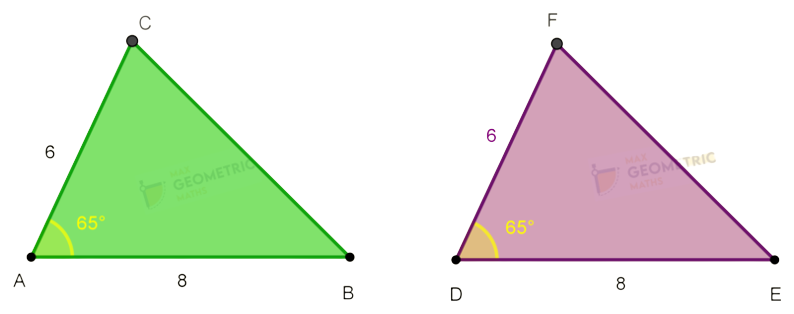
If any pair of corresponding sides and their included angles are equal, then the triangles are congruent
You can observe that,
AB = DE = 8
In Δ ABC & Δ DEF,
∠BAC = ∠EDC = 650
AC = DF = 6
The corresponding pair of sides & their included angle are equal.
Hence Δ ABC ≅ Δ DEF
Postulate 3
CONGRUENT TRIANGLES
ASA Theorem (Angle-Side-Angle)
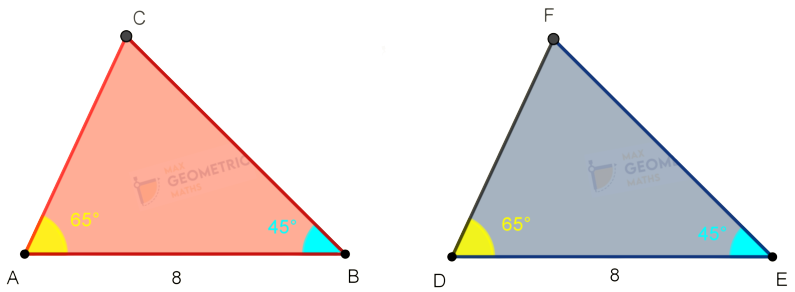
If any two angles and their included side are equal in the triangles, then the triangles are congruent.
You can observe that,
In ΔABC ΔDEF,
∠BAC=∠EDF = 650
AB = DE = 8
∠ABC=∠DEF = 450
The corresponding pair of angles & their included side are equal.
Hence ΔABC ≅ ΔDEF
Postulate 4
CONGRUENT TRIANGLES
AAS Theorem (Angle-Angle-Side)
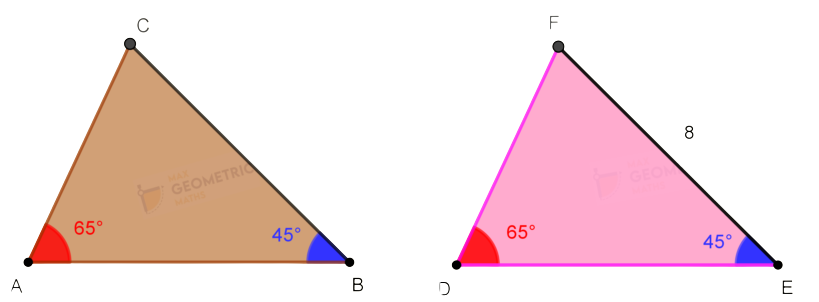
If two angles and one side of a triangle is equal to two angles & the corresponding side of the other triangle, then the triangles are congruent.
You can observe that,
In ΔABC ΔDEF,
∠BAC = ∠EDC = 650
∠ABC=∠DEF = 450
BC = EF = 8
Hence Δ ABC ≅ Δ DEF
Postulate 5
CONGRUENT TRIANGLES
RHS Theorem (Right Angle-Hypotenuse-Side)
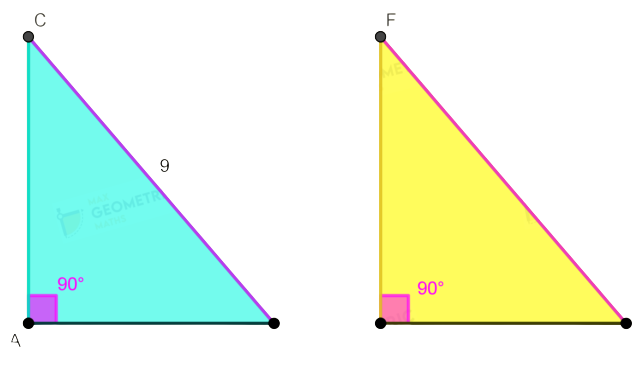
Two triangles are congruent if the hypotenuse & one side of a triangle is equal to the hypotenuse & the corresponding side of the other triangle.
You can observe that,
In right triangles ΔABC & ΔDEF,
∠BAC=∠EDF = 900
BC = EF = 9
AB = DE = 6
The hypotenuse & one side of ΔABC is equal to the hypotenuse & the corresponding side of ΔDEF.
Hence ΔABC ≅ ΔDEF
Some Standard Results
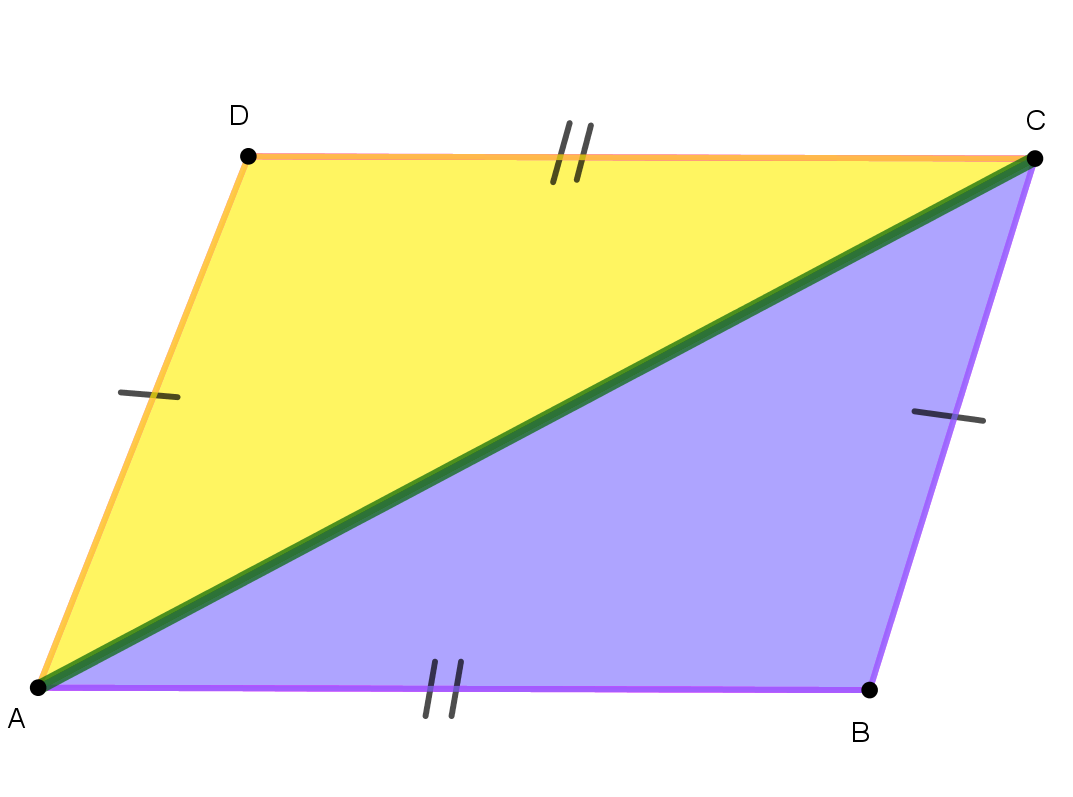
Result:
A diagonal of a parallelogram divides it into two congruent triangles
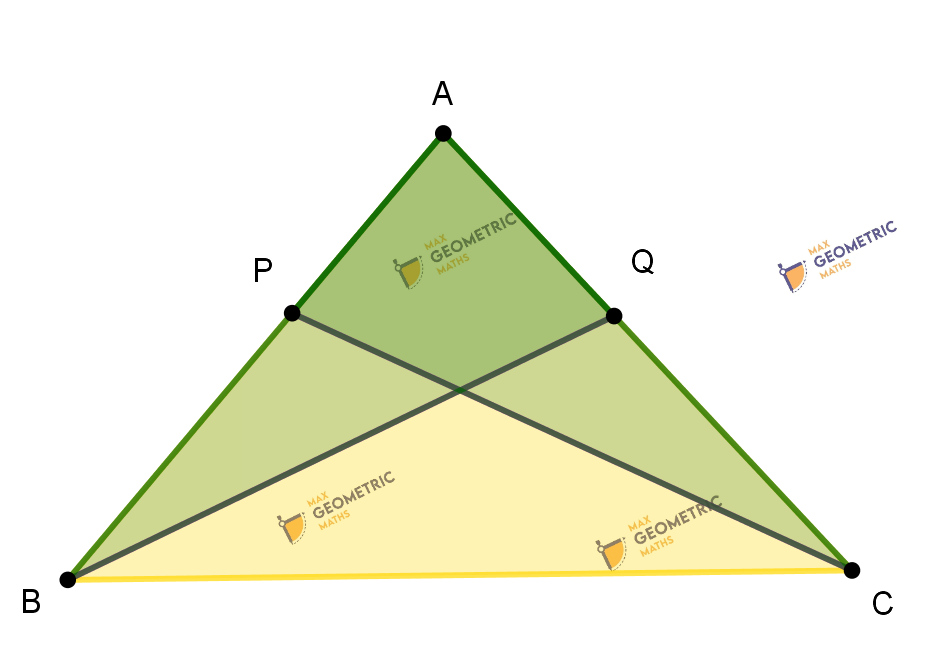
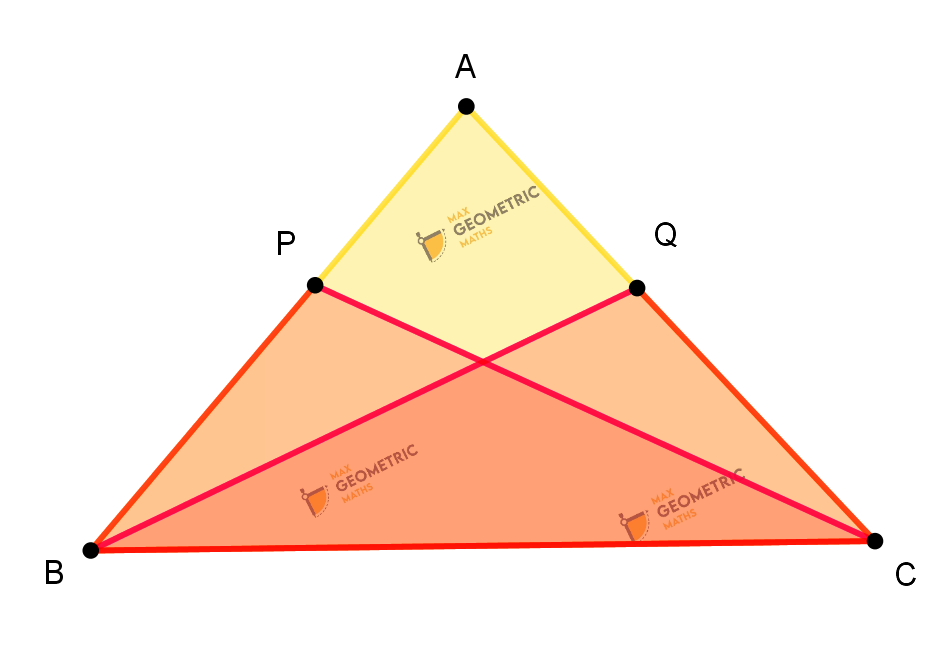
Result:
In ABC, AB & AC are equal. P & Q are points on AB & AC respectively such that AP = AQ. Then
- 1. Triangles APC & AQB are congruent.
- 2. Triangles BPC & CQB are congruent.
Similar Triangles
Two triangles are similar if their corresponding interior angles are equal and corresponding sides are proportional.
(i.e., Triangles are of same shape).
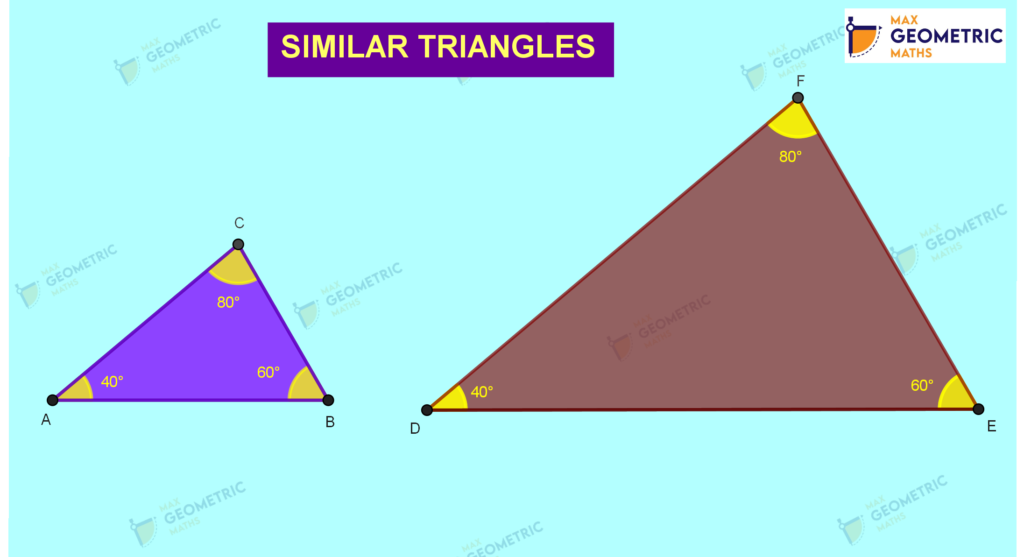
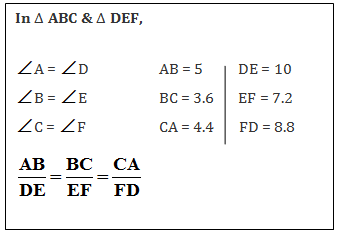
Notation for Similarity:
Δ ABC ‘is similar to’ Δ DEF is notated as Δ ABC ∼ Δ DEF
(It has to be expressed using correct correspondence of their vertices)
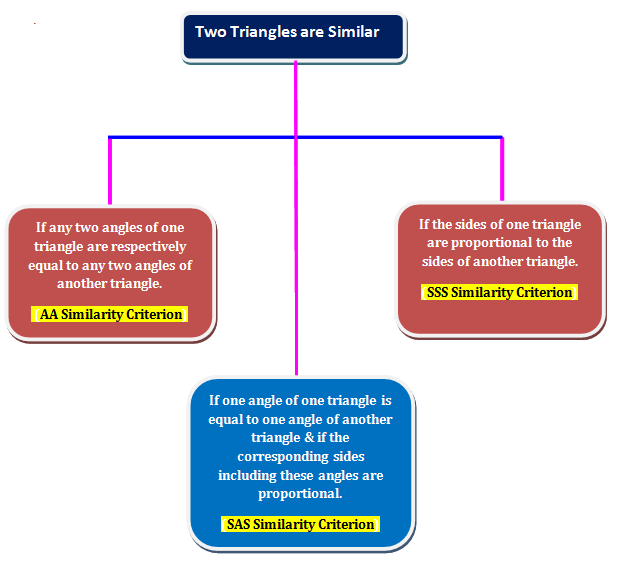
Similar Triangles Criterion
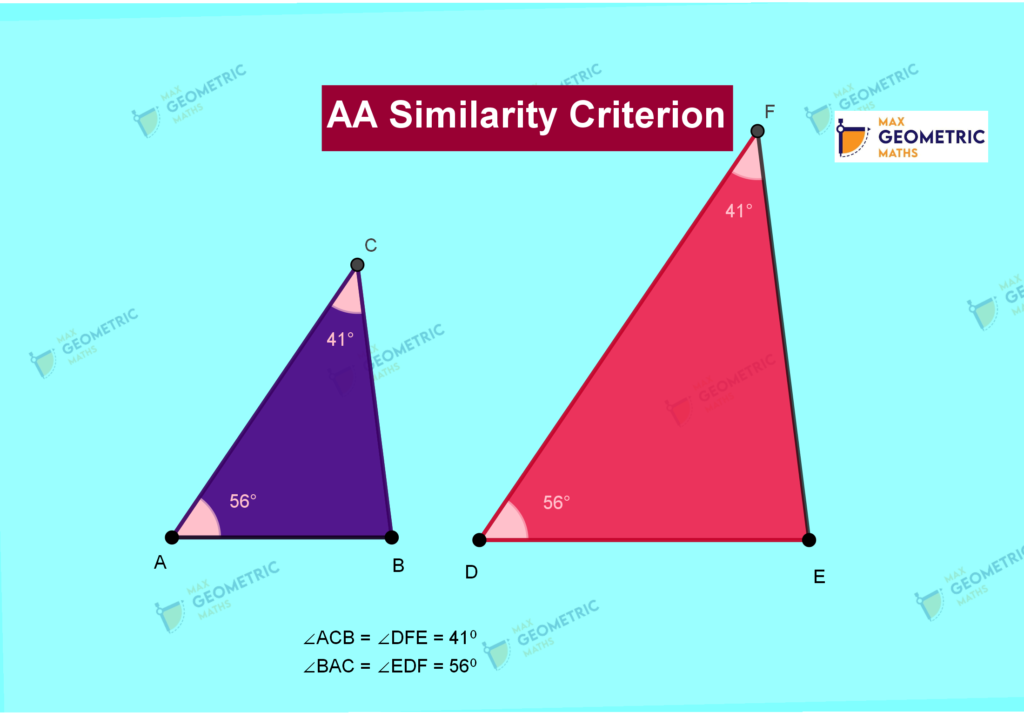
- 1. AA Similarity Criterion
- 2. SSS Similarity Criterion
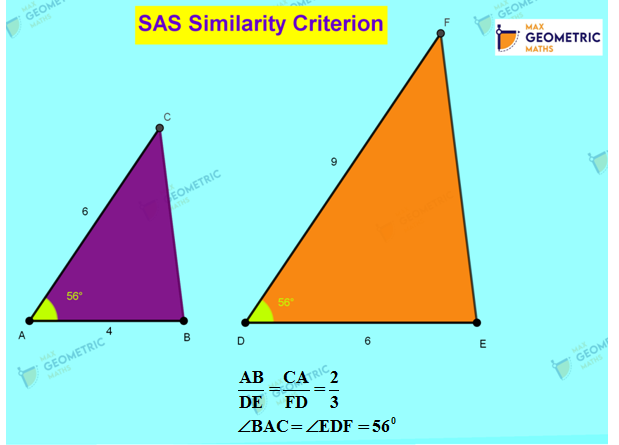
- 3. SAS Similarity Criterion
Similarity Criterion 1
Similarity Criterion 2
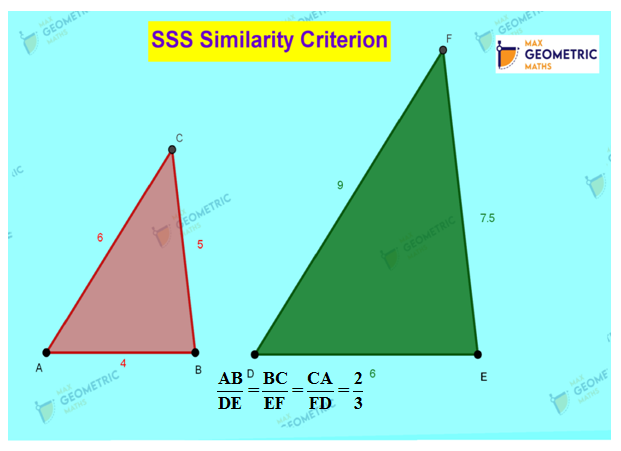
Similarity Criterion 3
SOME STANDARD RESULTS ON SIMILAR TRIANGLES:
Result :
If a perpendicular is drawn from the vertex of a right angled triangle to its hypotenuse, then the triangles on each side of the perpendicular are similar to the whole triangle.
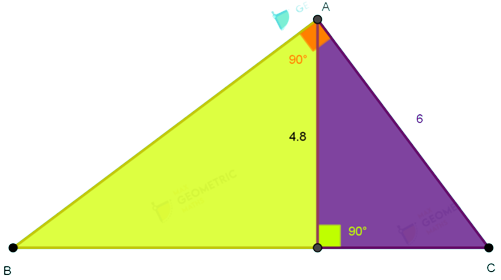
Δ ABC ~ Δ DBA
Δ ABC ~ Δ DAC
Δ DBA ~ Δ DAC
Note:
There are five line segments AB, AC, AD, BD & DC. If any of the two line segments are known, then the remaining can be found using the identities.
AD2 = BDxDC
AB2 = BDxBC
AC2 = CDxCB
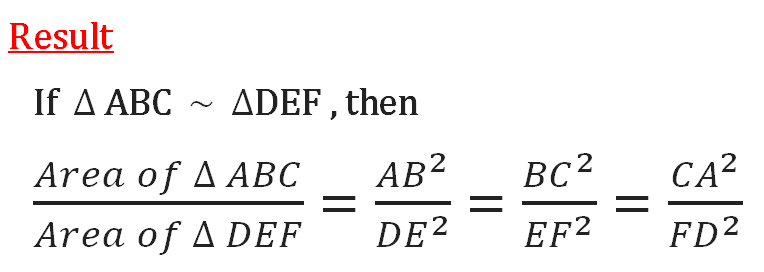
Result :
If two triangles are similar, then the ratio of the corresponding sides is equal to the ratio of their corresponding altitudes.
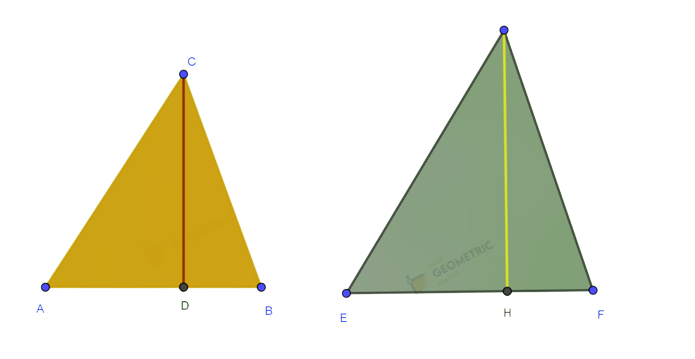
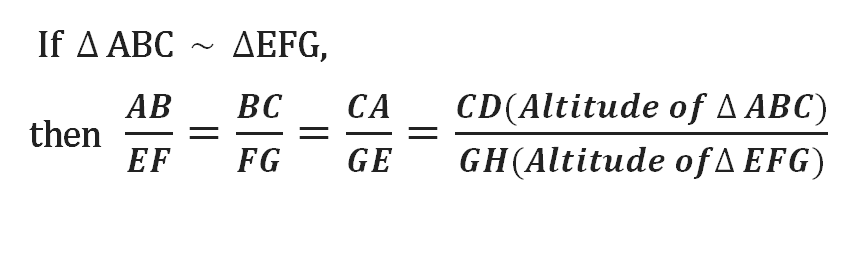
Result :
If two triangles are similar, then the ratio of the corresponding sides is equal to the ratio of their corresponding perimeters.
DE || BC
Δ ABC ~ Δ ADE
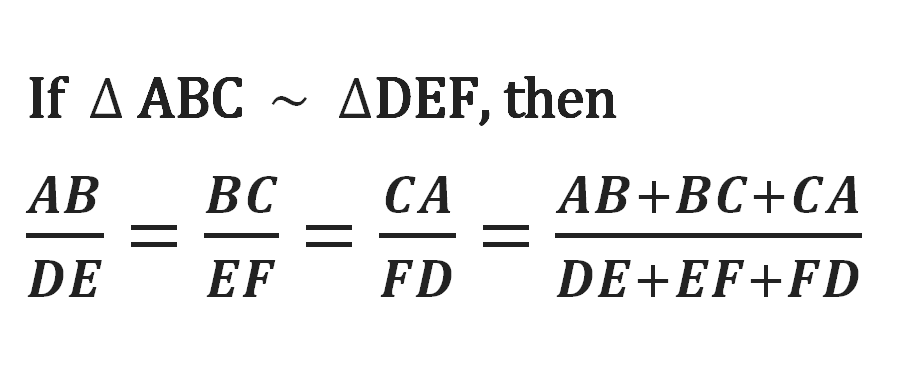
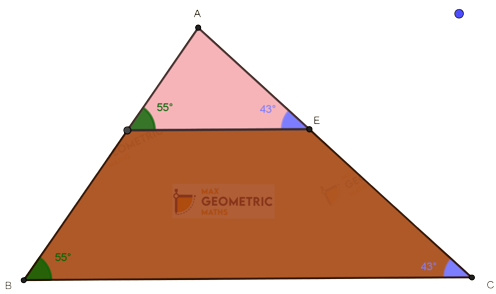
In A ABC, as DE is parallel to BC
∠ABC= ∠ADE =550
∠ACB = ∠AED = 430
By AA Similarity Criterion,
Δ ABC ~ Δ ADE
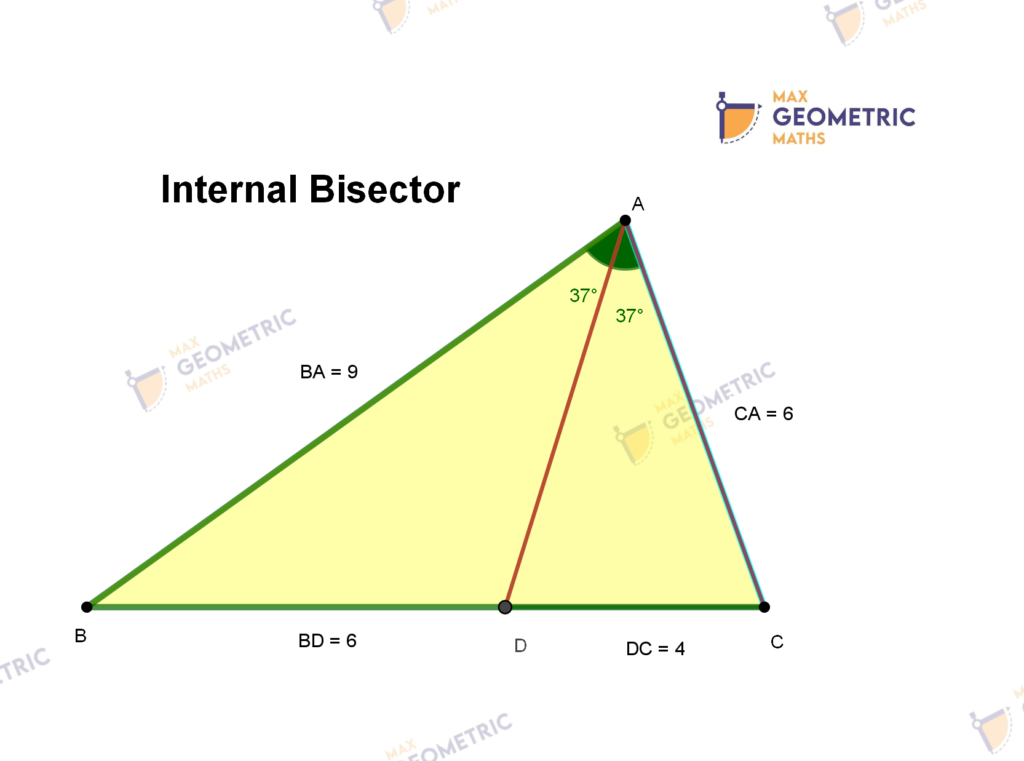
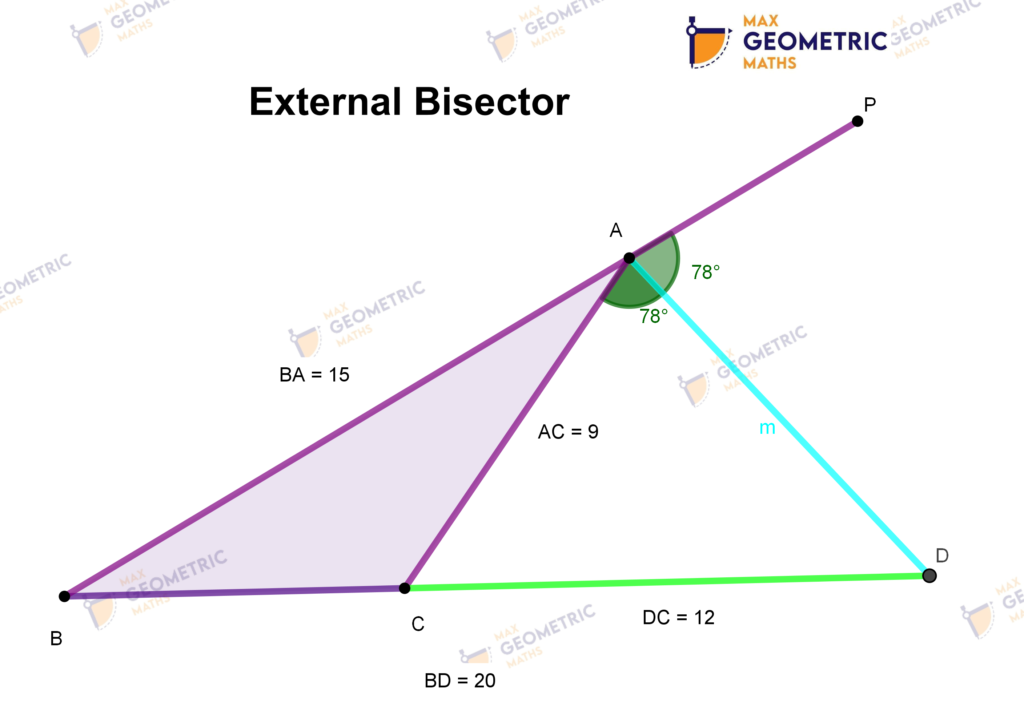
Angle Bisector Theorem
The internal (external) bisector of an angle of a triangle divides the opposite side internally (externally) in the ratio of the corresponding sides containing the angle.
In ΔABC, if AD is the internal bisector of ∠BAC which meets BC at D
(Or)
If AD is the external bisector of ∠BAC which meets BC produced at D, then
BD/DC = AB/AC
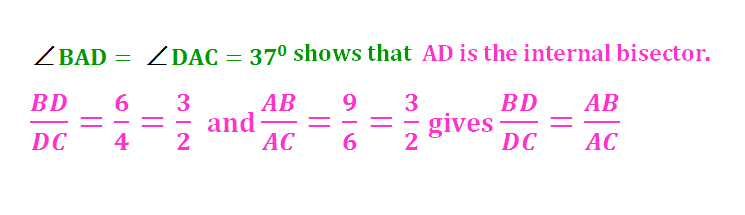
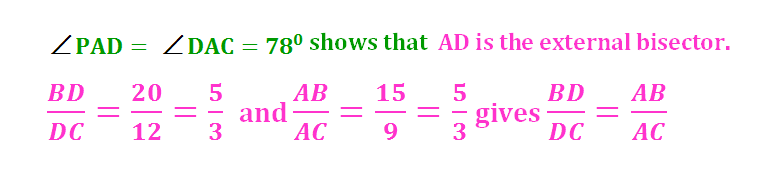
Converse of Angle Bisector Theorem
If a straight line is drawn through one vertex of a triangle divides the opposite side internally or externally in the ratio of the other two sides, then the line bisects the angle internally or externally at the vertex.
Internally
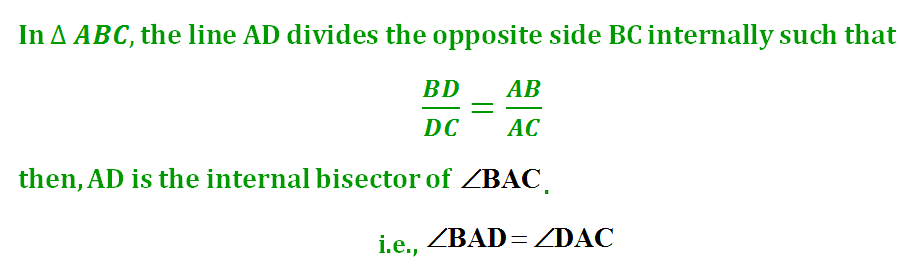
Externally

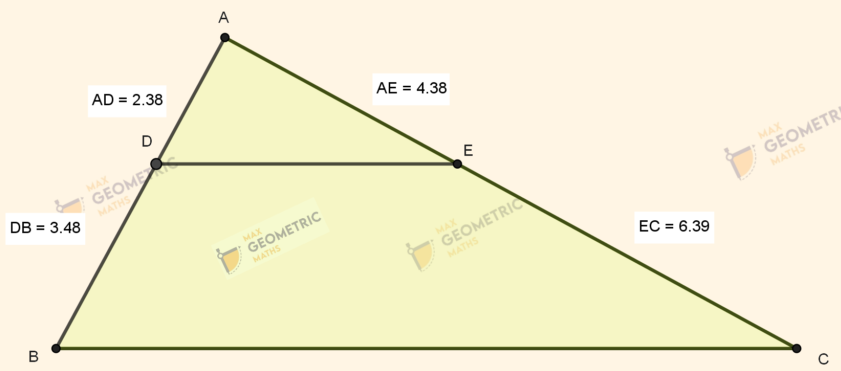
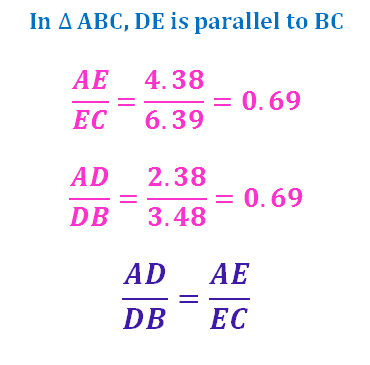
Basic Proportionality Theorem
Basic Proportionality Theorem (abbreviated as BPT).
It is attributed to the Greek Mathematician Thales. So, this theorem is also known as Thale’s Theorem.
STATEMENT :
If a straight line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.

Basic Proportionality Theorem
Converse of Basic Proportionality Theorem
STATEMENT:
If a straight line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.

Ceva’s & Menelaus Theorem
CEVIANS:
Cevians play a very significant role in proving many geometric results. In a triangle, Cevian is a line joining a vertex to its opposite side.
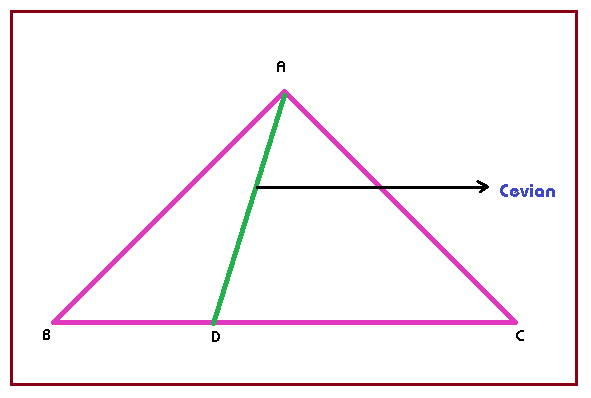
Special Cevians
- Medians
- Altitudes
- Angle bisectors
- Perpendicular bisectors (only in equilateral triangle & in an Isosceles triangle for non-concurrent lines).
Using Ceva’s Theorem, it can be easily proved that
- 1. Medians of a triangle are concurrent.
- 2. Altitudes of a triangle are concurrent.
- 3. Angle Bisectors of a triangle are concurrent.

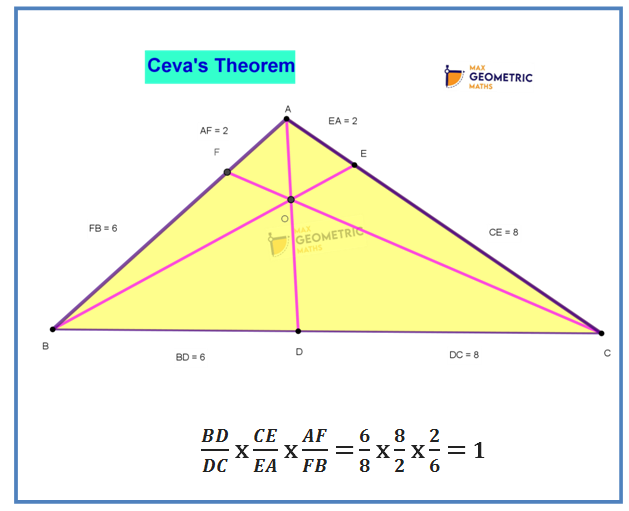
The concept of Concurrency in detail & Ceva’s Theorem with Proof
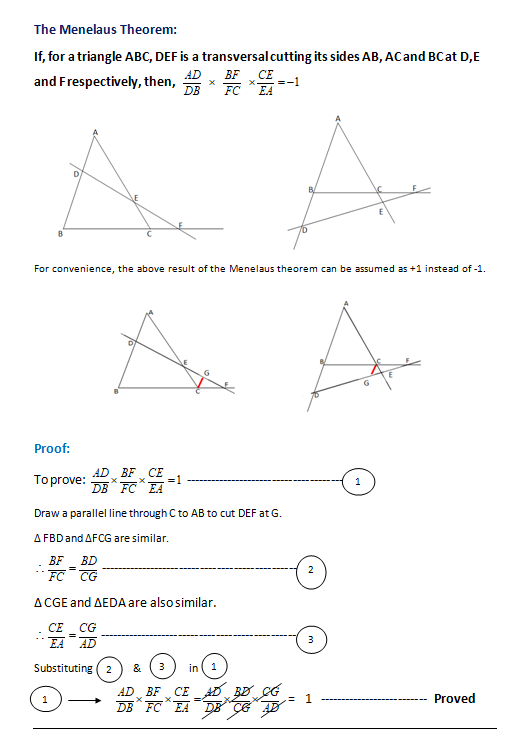
Menelaus Theorem
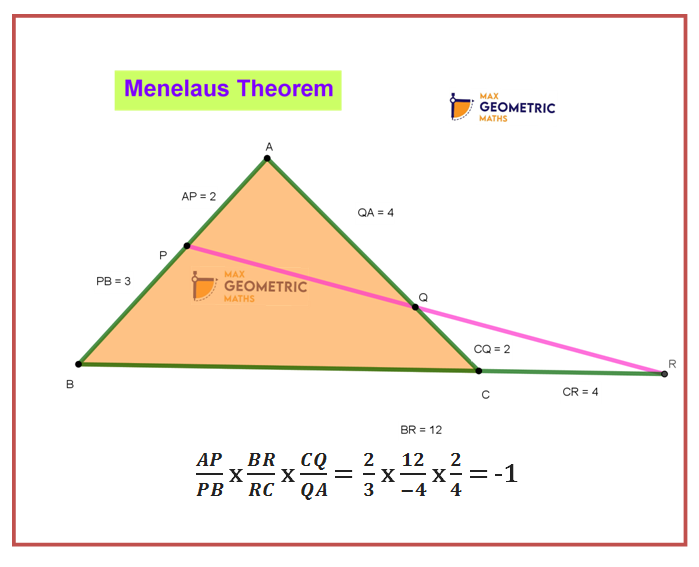

The above condition can be easily remembered as
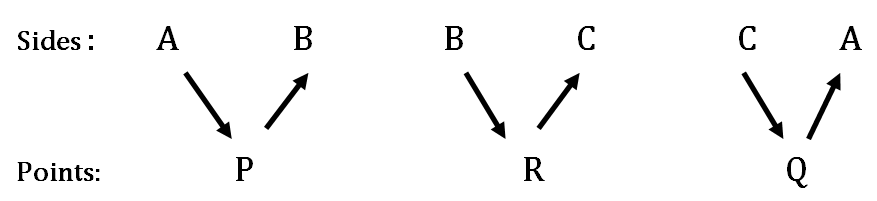
Author’s Creation in Triangles
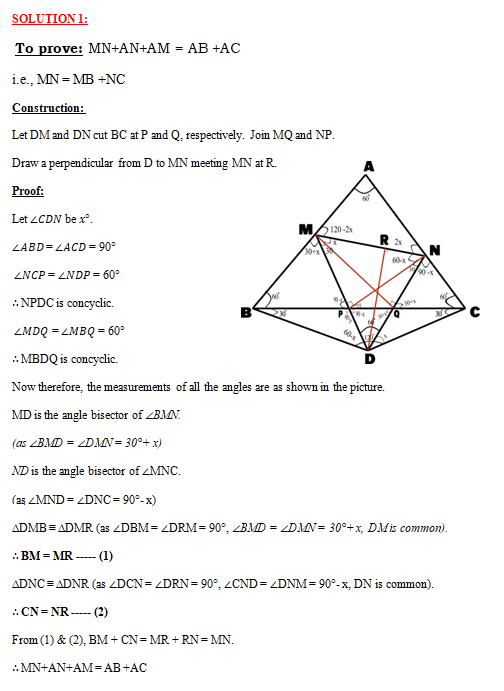
1. Question:
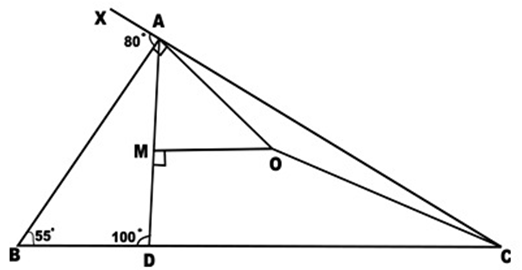
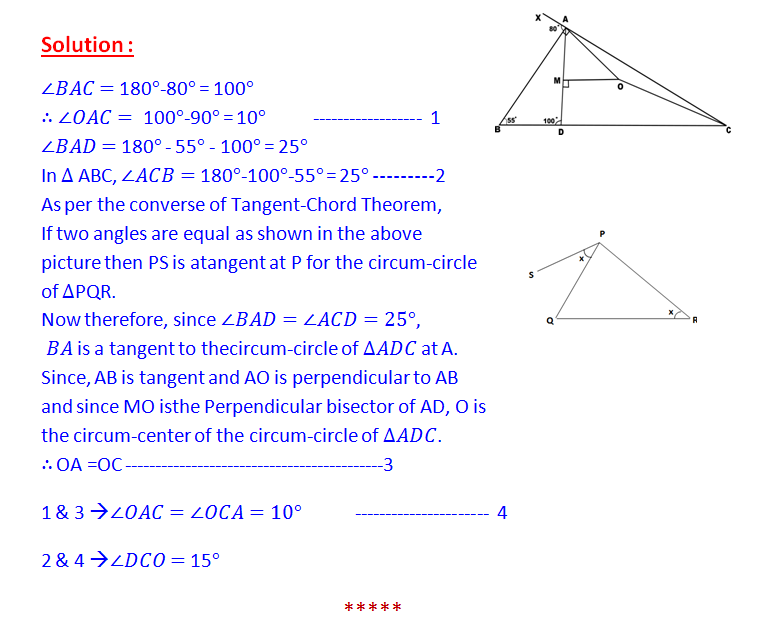
In Δ ABC, ∠B = 55°. AD is a cevian such that ∠ADB = 100°. CA is produced to X and ∠BAX = 80°. M is the midpoint of AD. The perpendicular line drawn to AD through M and the perpendicular line drawn to AB through A meet at O. Find the measurement of ∠DCO.
2. Question:
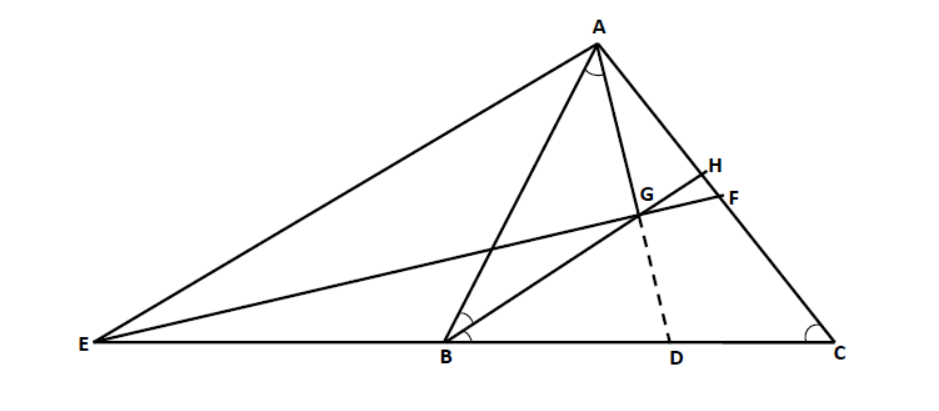
The story behind the problem: The author received the problem ‘In Δ ABC, BH is the bisector of ∠ B meeting AC at H. CB is produced to E such that AB =BE. F is the midpoint of AC. EF and BH meet at G and AG is joined. Prove that ∠BAG=∠C’ from his Vijayawada Friend Mr. Lakshmana Moorthy. He started to solve the problem by his favourite angle bisector theorem & Menelaus theorem but he could not complete it because of his busy schedule. So he forgot about that problem later. After two months, during lock down all of a sudden he remembered that he didn’t solve the problem. So he immediately rang up to his friend and enquired whether anyone solved it in these two months gap. But his friend replied that no one could solve it. Again, he sat with that problem & found the solution. His friend was very much excited when he heard that our author has solved the problem which no geometricians could solve. Based on the problem, he received from his friend, he extended the result & found the below result as its corollary.
In Δ ABC, BH is the bisector of ∠ B meeting AC at H. CB is produced to E such that AB =BE. F is the midpoint of AC. EF and BH meet at G and AG is joined. Prove that AG = AH
3. Question:

4. Question:
A straight line makes positive intercepts on the x & y axis at A & B respectively. The distance between A & B is 70 units. Another straight line y = x intersects AB at C and AC : CB = 4:3. Find the equation of the straight line AB.
6. Question:
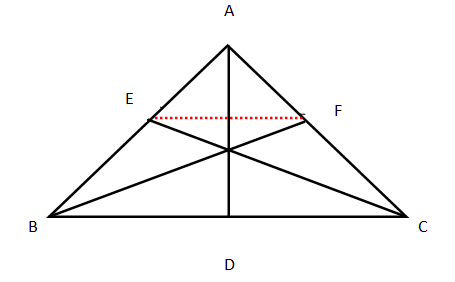
For the below result, the Geometricians across the world have given their own lengthy proofs. But the author has proved this result very simply in just two steps using ceva’s theorem.
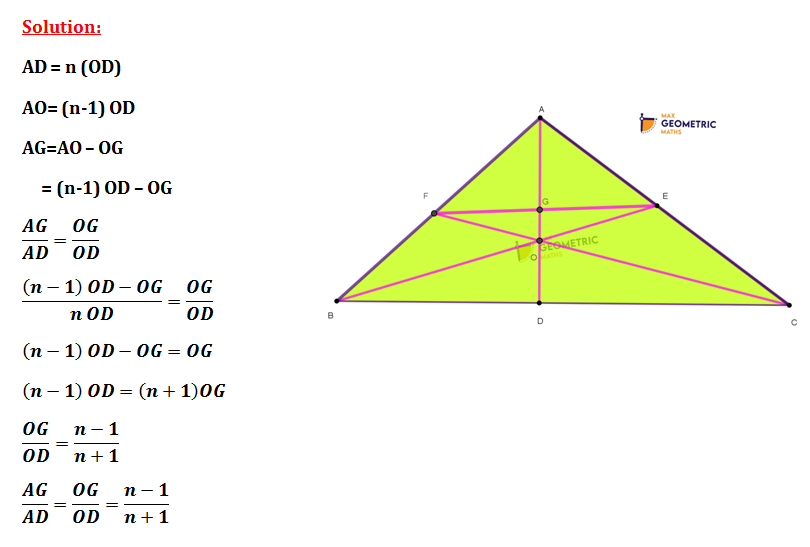
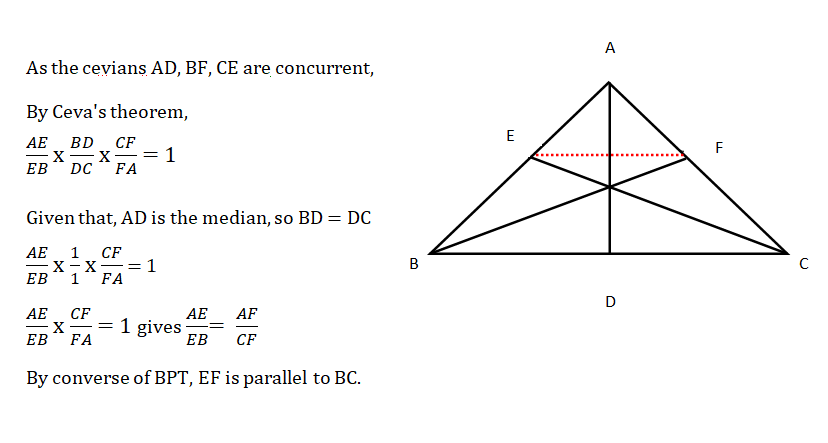
In Δ ABC, AD is the median meeting BC at D. ‘O’ is a point on AD. If cevians drawn from B & C through ‘O’ meet AC & AB respectively at F & E, then EF is parallel to BC
7. Question:
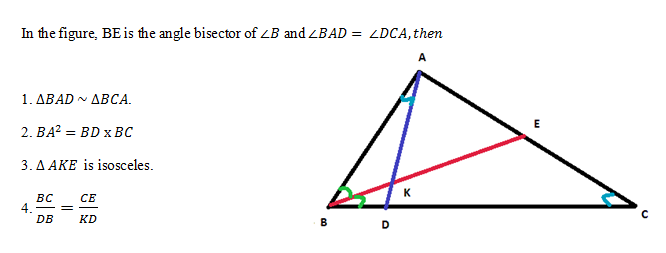
8. Question:
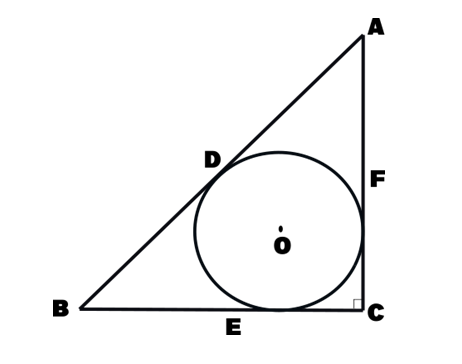
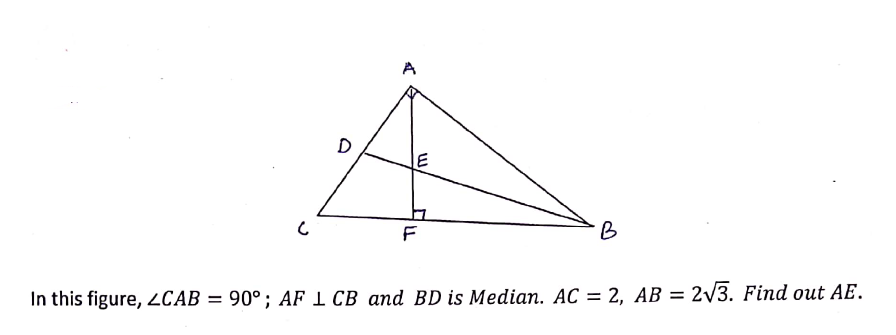
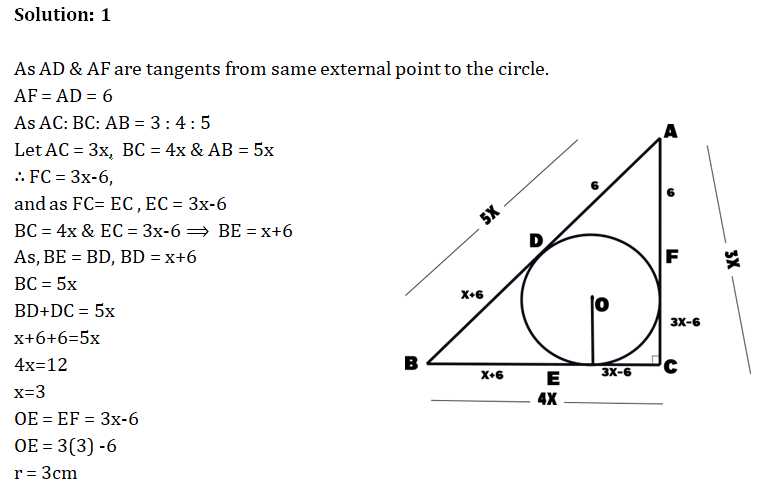
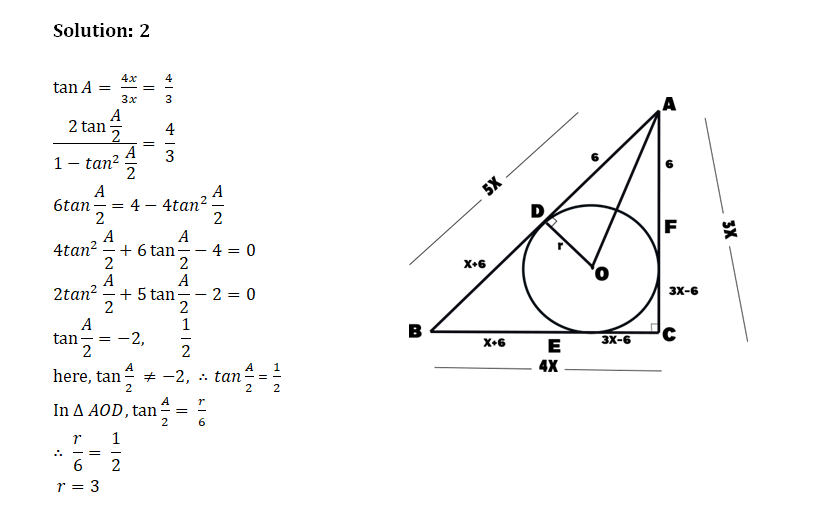
ABC is a triangle circumscribing a circle of radius ‘r’ cm. Let D, E, F be the point of contracts as shown in the figure. If AD = 6 cm & AC : BC : AB = 3 : 4 : 5. Find the value of r
9. Question:
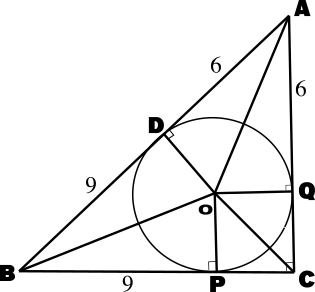
A triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments AD & DB into which AB is divided by the point of contact D are of lengths 6 cm and 9 cm respectively. Find the sides AC & BC.
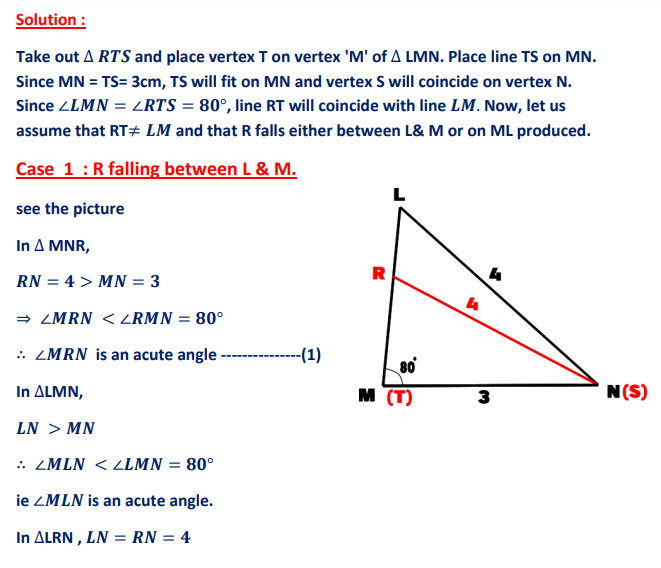
10. Question:
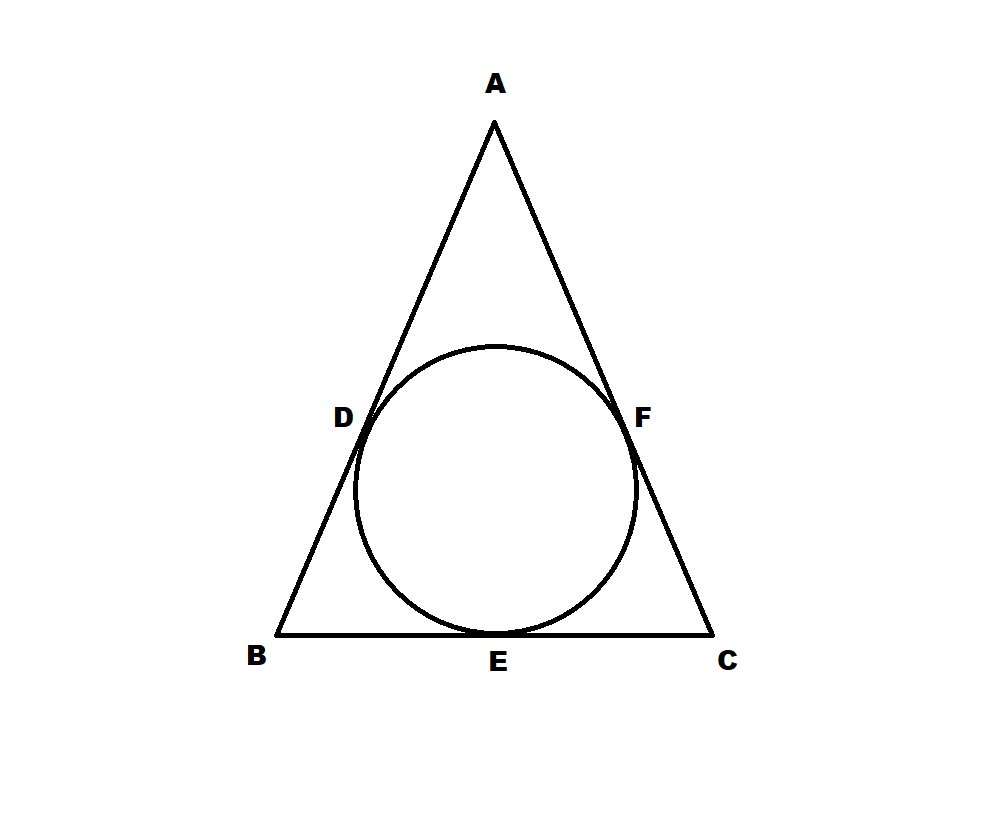
ABC is an ordinary triangle, AB:BC:CA = 7:5:8. Its incircle touches AB at D, if AD = 5cm, find the radius of the incircle.
11. An Essay on Pythagoras Theorem




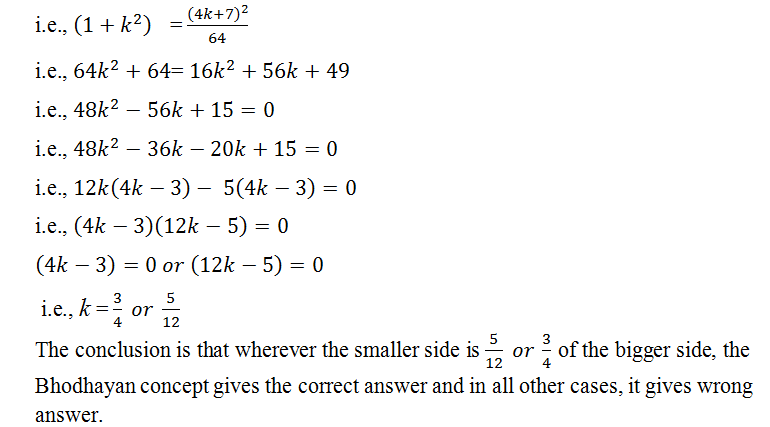
Dr.M.Raja Climax
Founder Chairman, CEOA
12. Question:
In ∆ 𝑨𝑩𝑪, BP & CQ are cevians intersecting each other at O. Area ∆ 𝑩𝑶𝑸 = 𝒂 ,𝑨𝒓𝒆𝒂 ∆ 𝑩𝑶𝑪 = 𝒃 𝒂𝒏𝒅 𝑨𝒓𝒆𝒂 ∆ 𝑪𝑶𝑷 = 𝒄. Find the area of Quadrilateral AQOP in terms of a, b & c
13. Question:
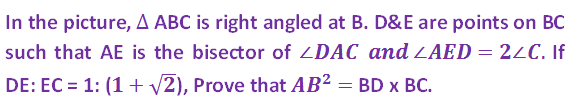
14. Question:
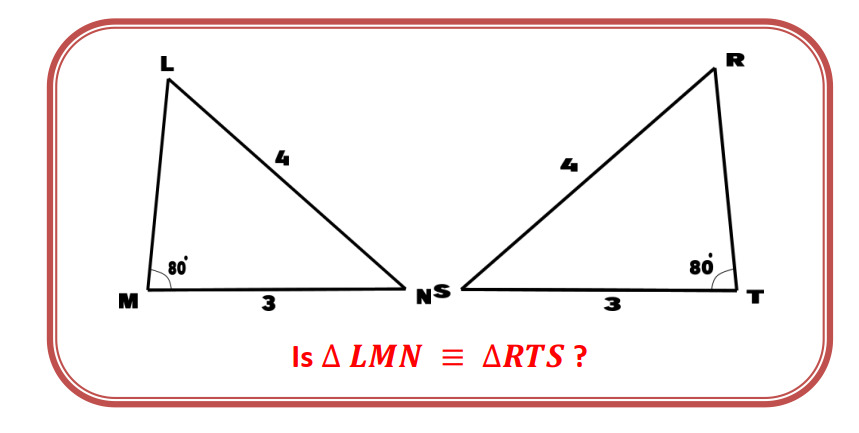
15. An article on Congruency

16. Question:
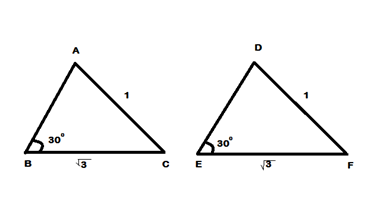
In ΔABC & ΔDEF, BC=EF=√3 , AC=DF=1, ∠ABC=∠DEF=30°. Check whether the triangles are congruent?
17. Question:
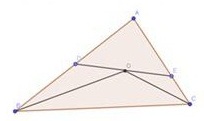
In a ΔABC, the bisectors of ∠B & ∠C meet at 0.DE isa straight line drawn through O such that AD=AE. Prove that DE2= 4 (BD x CE)
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA
18. Question:
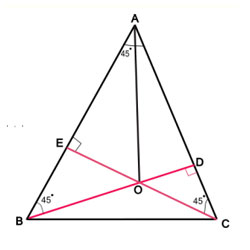
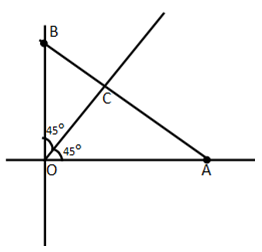
Here is an interesting discovery from me. Draw any triangle ABC with A = 45 degree. Find out its orthocentre O. Now, OA = BC. You will get this result irrespective of the lengths of AC, AB & BC.
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA
Author’s Solution for Challenging Problems in Triangles
1. Question:
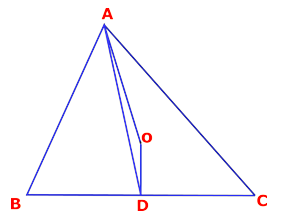
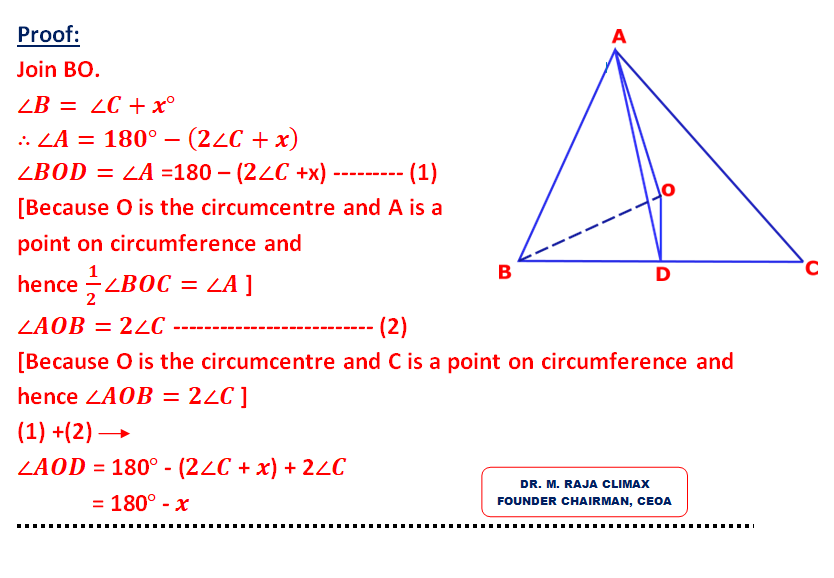
In Δ ABC, ∠B — ∠C =x°. O is the circumcenter and ‘D’ is the midpoint of BC. Prove that ∠AOD = 180° — x°
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA
2. Question:
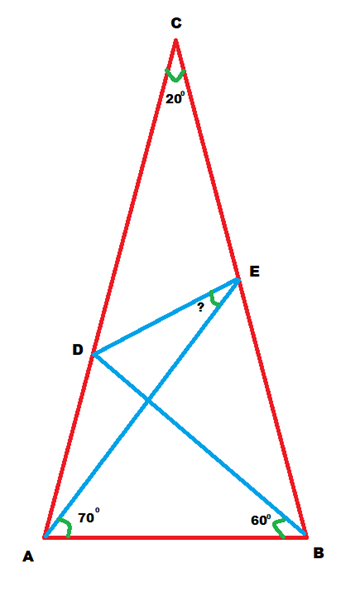
In Δ ABC, AC=BC and ∠C=20°. If D & E are points on AC & BC such that ∠EAB = 70° & ∠DBA = 60°, then find ∠DEA.
For this problem, the author has given two different solutions one using geometry and the other using trigonometry.
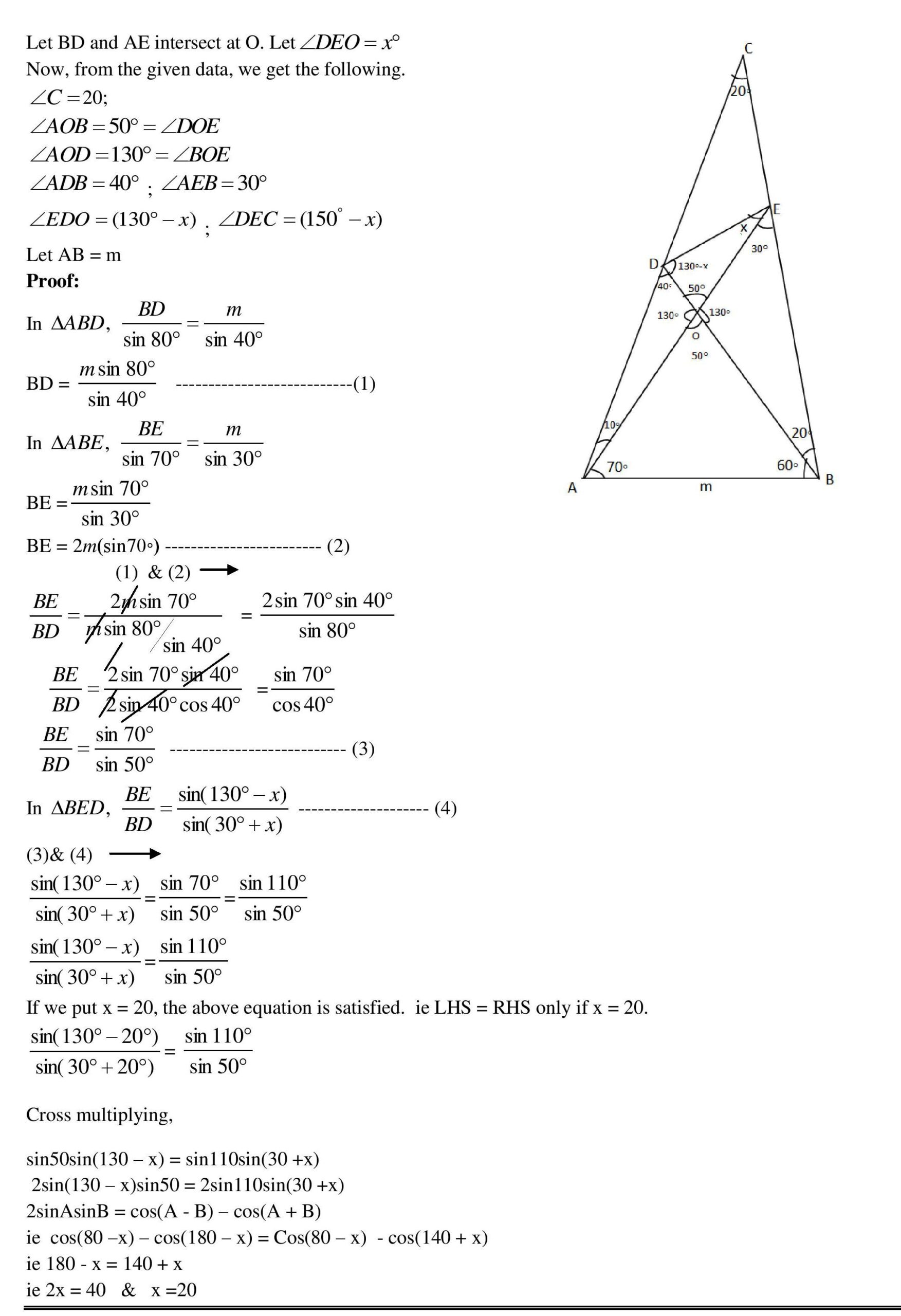
3. Question:
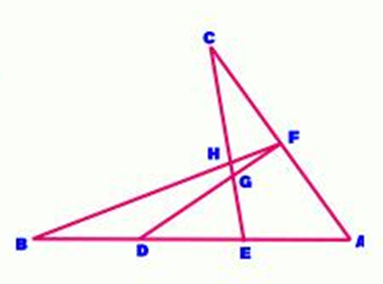
Give non-collinear points A,B,C, segment AB is trisected by points D & E, and F is the mid-point of segment AC. DF & BF intersect CE at G & H respectively.
If area of Δ DEG is 18 Sq.units, find the area of Δ FGH.
4. Question:
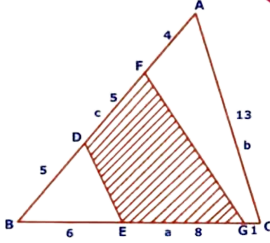
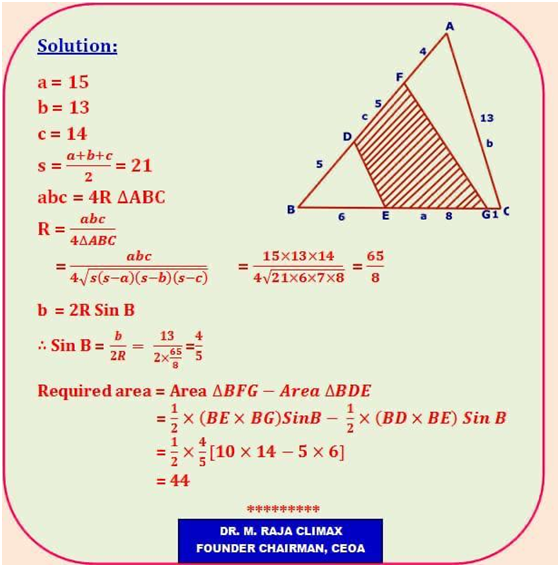
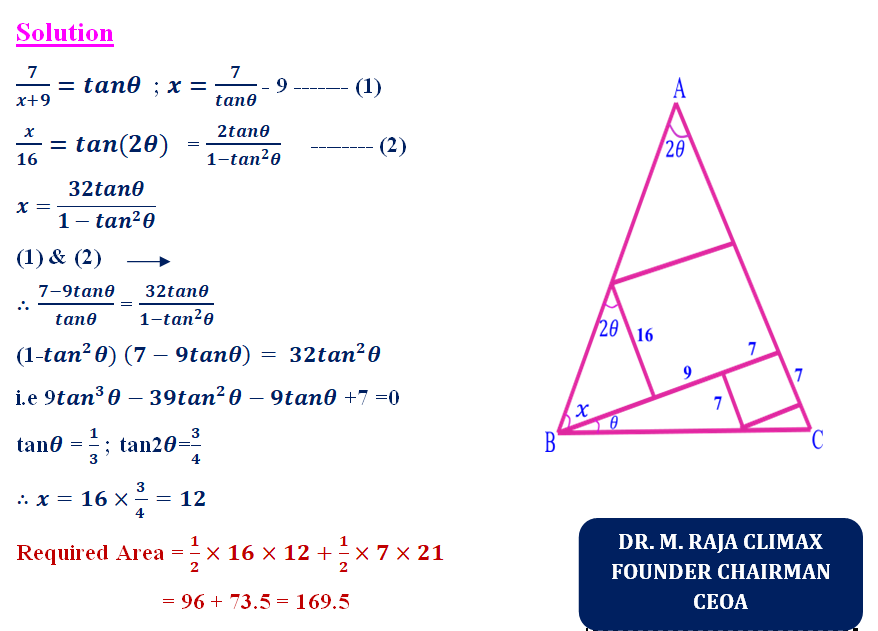
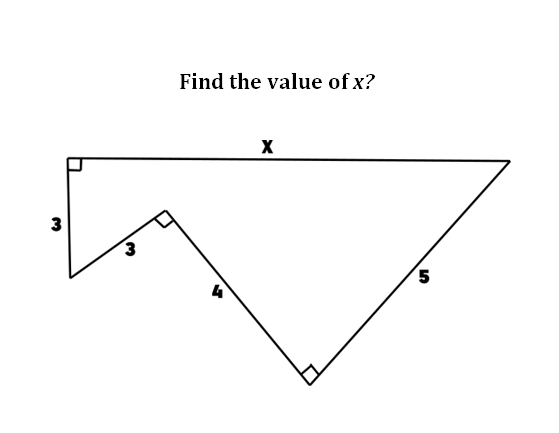
Find the area of the shaded region
5. Question:
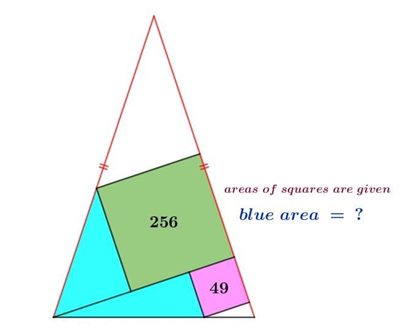
For this above Problem, You can find some lengthy & complicated solutions which is hard to follow in the net but our Author has given not one or two but three various Simple Solutions which can be viewed below.
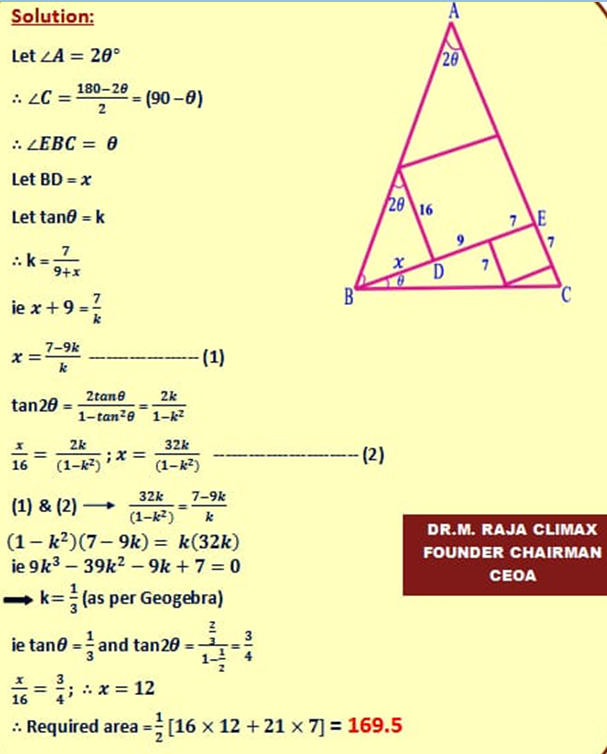
6. Question:
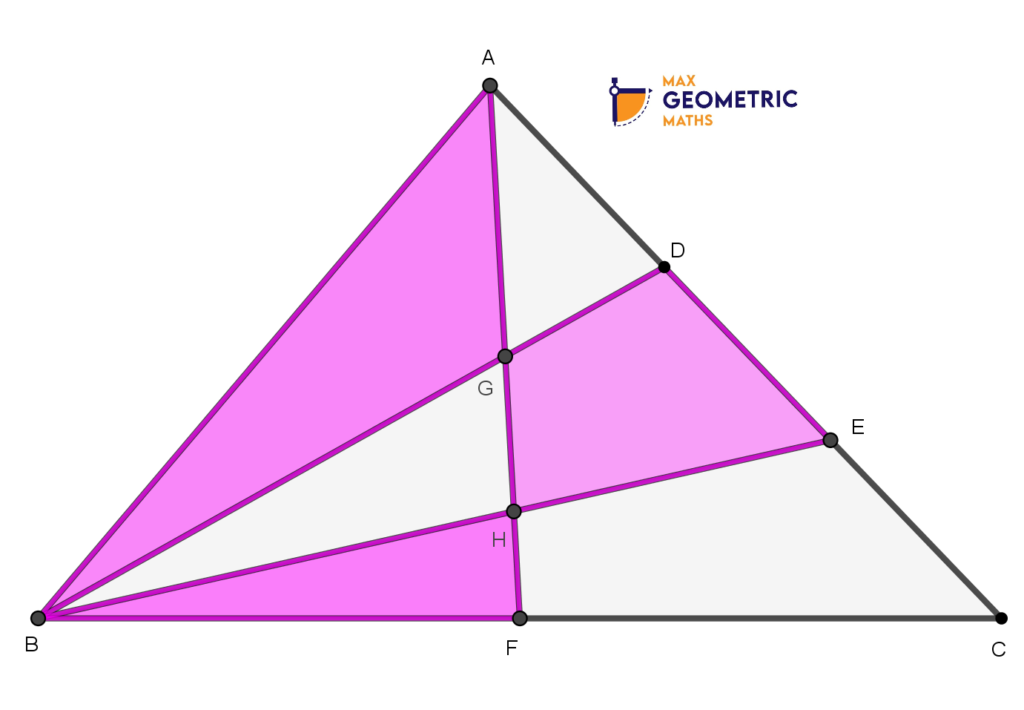
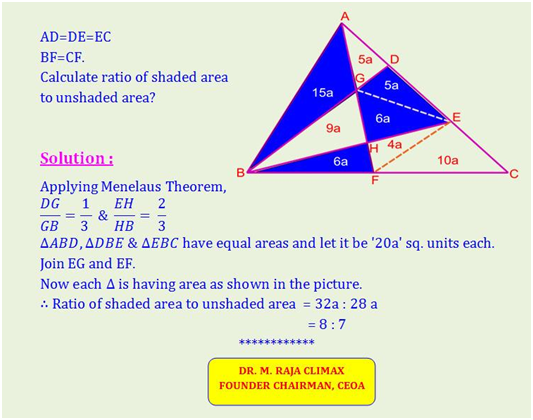
In Δ ABC, find the area of the shaded area to unshaded area if AD=DE=EC & BF=CF.
7. Question:
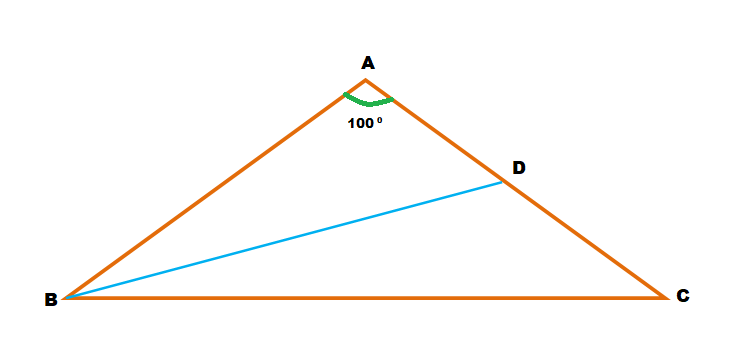
In Δ ABC, ∠A = 100º & AB = AC. The angle bisector of ∠B meets AC at D. Prove that BD + AD =BC
8. Question:
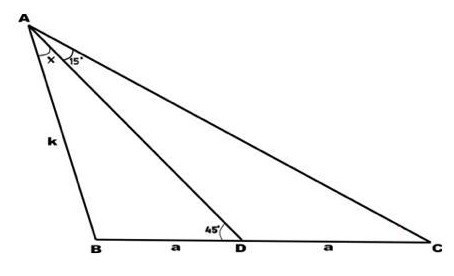
In ΔABC, AD is a median from A to BC such that ∠DAC=15° and ∠ADB=45º, find x
9. Author's Corollary 1
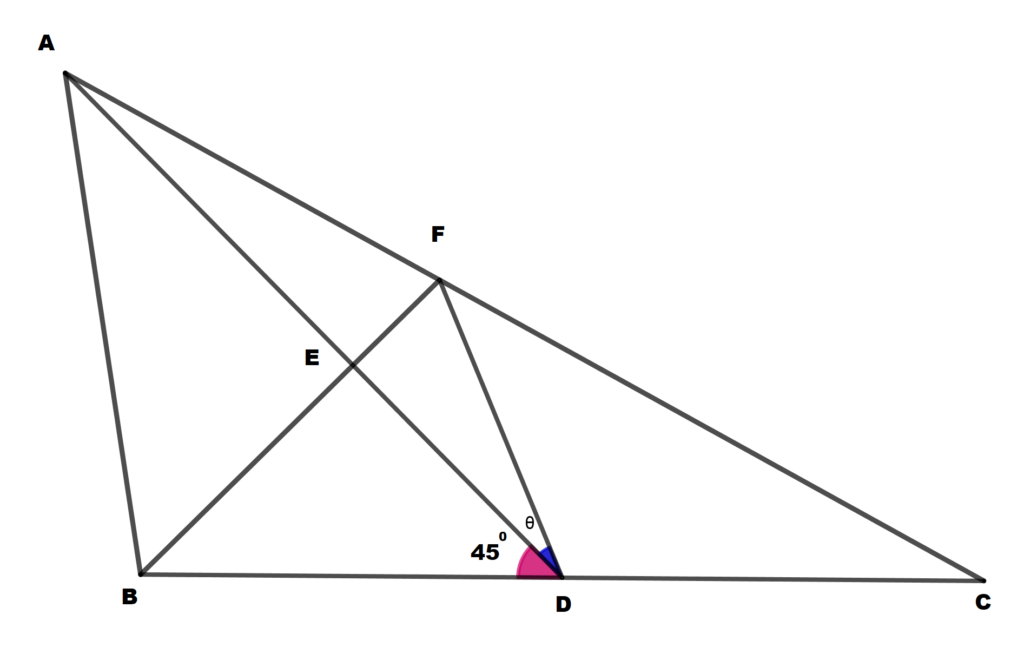
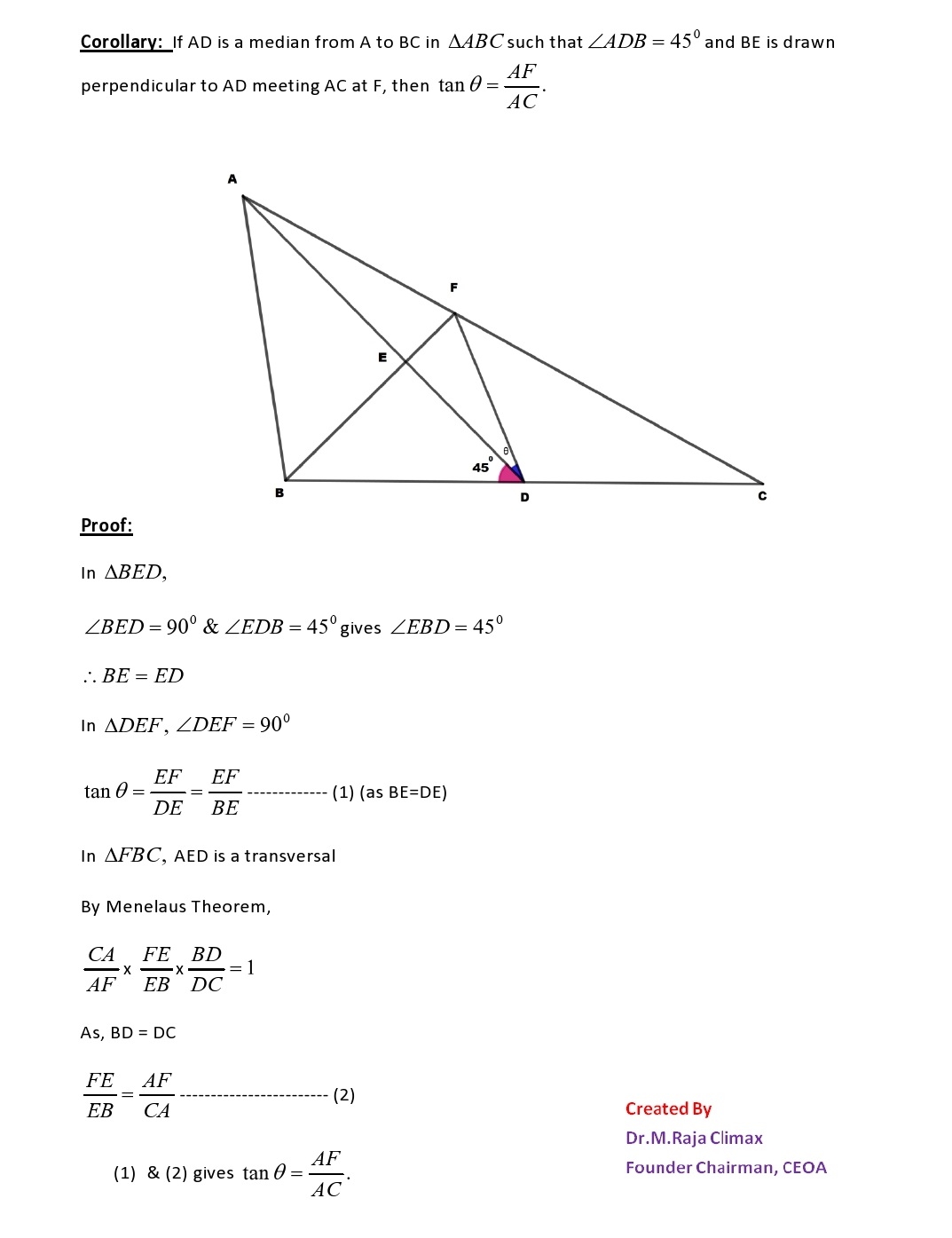
Corollary If AD is a median from A to BC in such that ∠ADB=45º and BE is drawn perpendicular to AD meeting AC at F, then tan θ = AF/AC
10. Author's Corollary 2
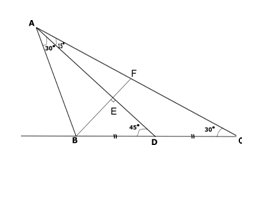
If AD is a median from A to BC in such that ∠ADB=45° and ∠DAC=15° .BE is drawn perpendicular to AD meeting AC at F, then AD x BF = 2 BD²
12. Question
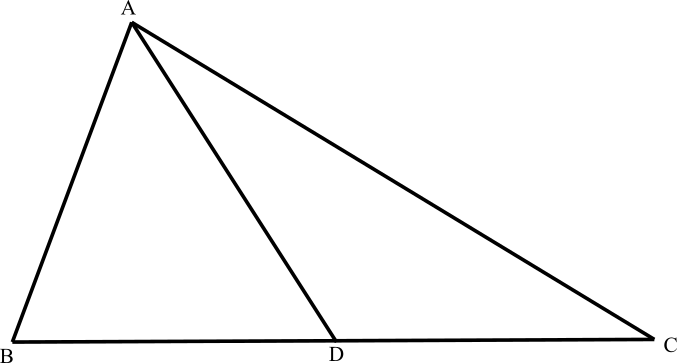
In triangle ABC, ∠B = 2∠C, if AD is the angle bisector such that DC = AB, then find angle A
13. Question
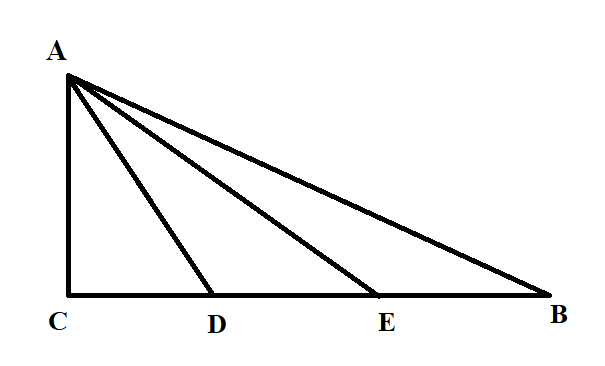
ABC is a triangle right angled at C. BC is divided by points D & E into three equal parts. Find the sum of the angles AEC, ADC & ABC if BC = 3AC.
14. Question
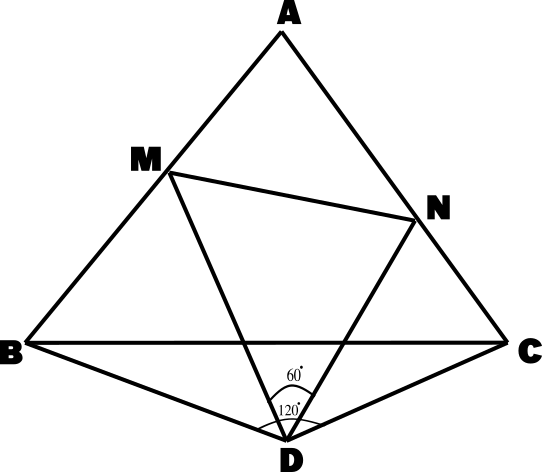
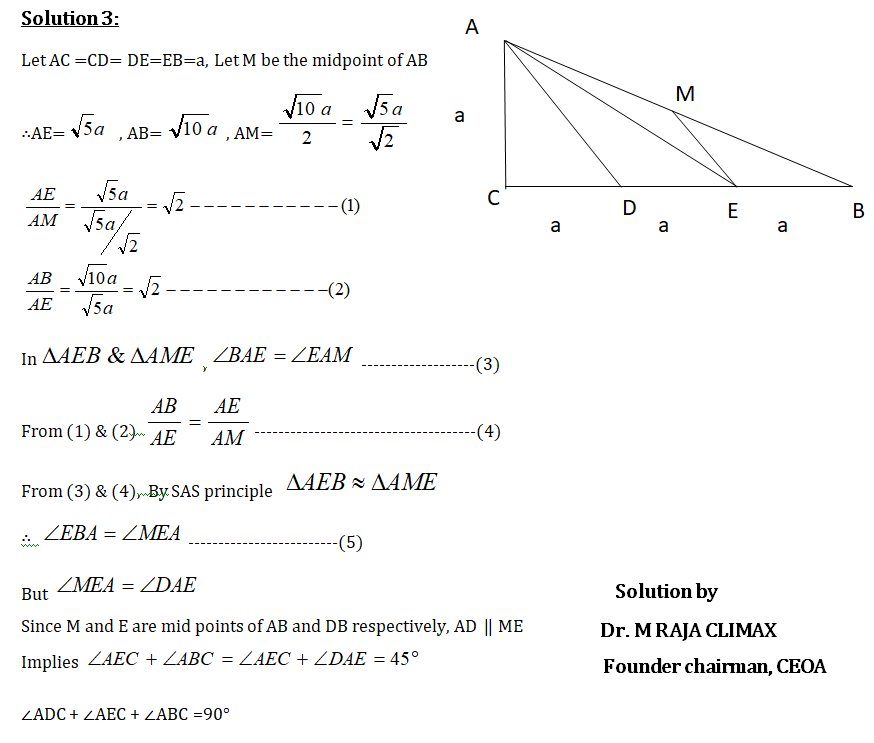
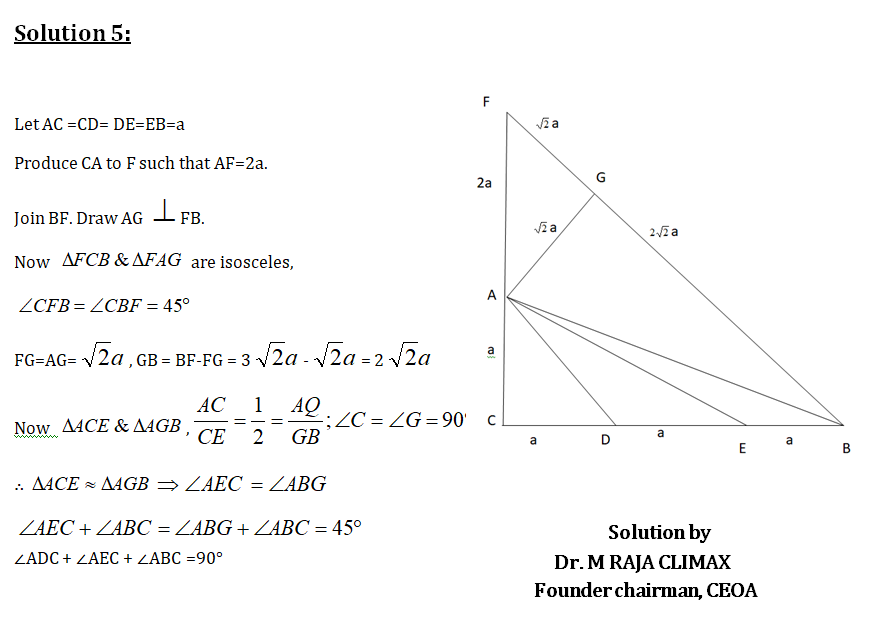
∆ ABC is an equilateral triangle. D is a point outside ∆ABC such that
BD=CD=a cm and ∠𝐵𝐷𝐶=120°.
M, N are points on AB, AC respectively such that ∠𝑀𝐷𝑁=60°.
Prove that MN+AN+AM = AB+AC.
Corollary
- 1. Triangles MDN, MBP, QDP & QCN are similar to each other.
- 2. ∠ANM = 2∠CDN
- 3. Triangles MQN & DCN are similar
- 4. Triangles MBD & MPN are similar
- 5. MNQP is concyclic
15. Question
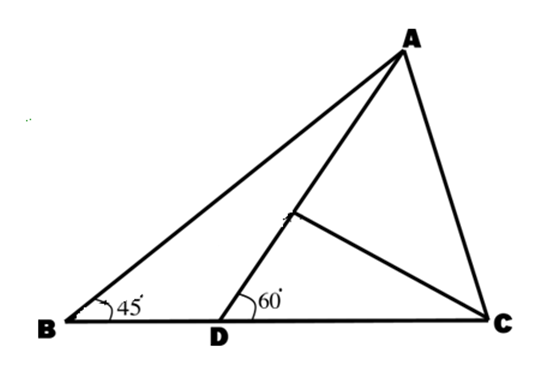
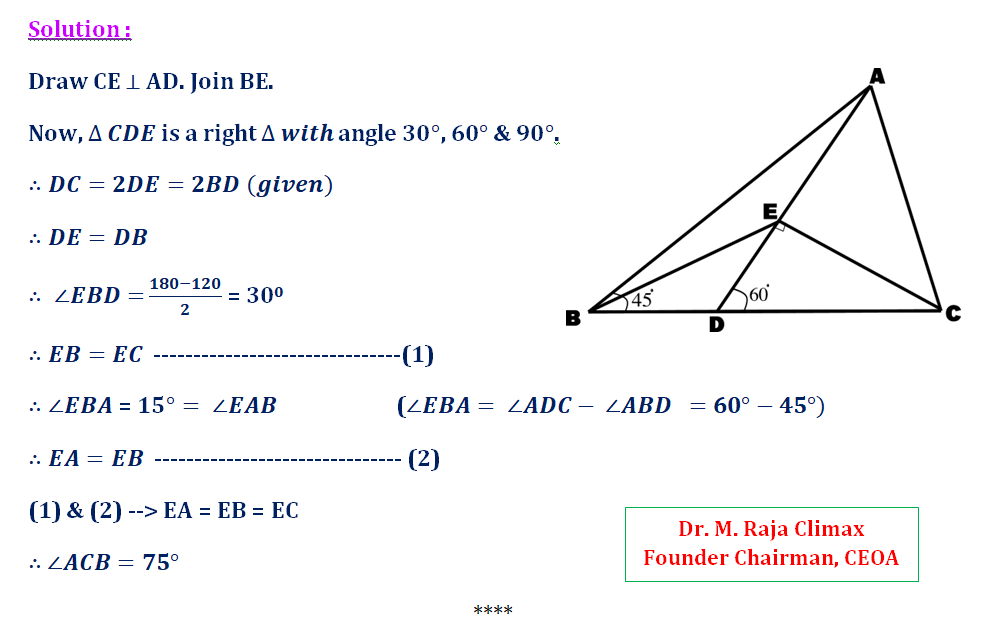
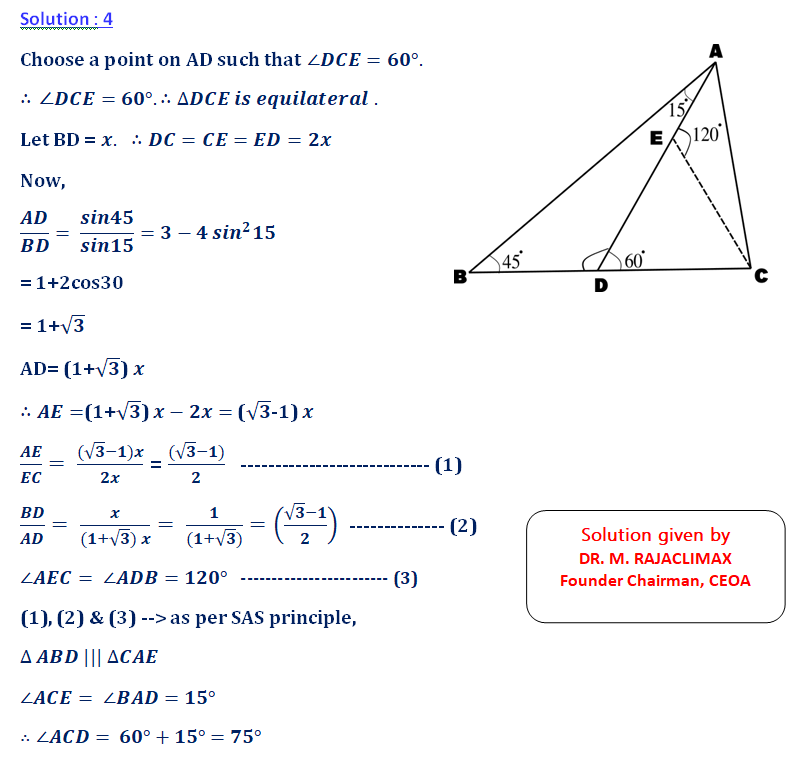
In, ΔABC, ∠ABC = 45º, AD is a cevian meeting BC at D such that DC = 2BD and ∠ADC = 60º, find ∠ACB.
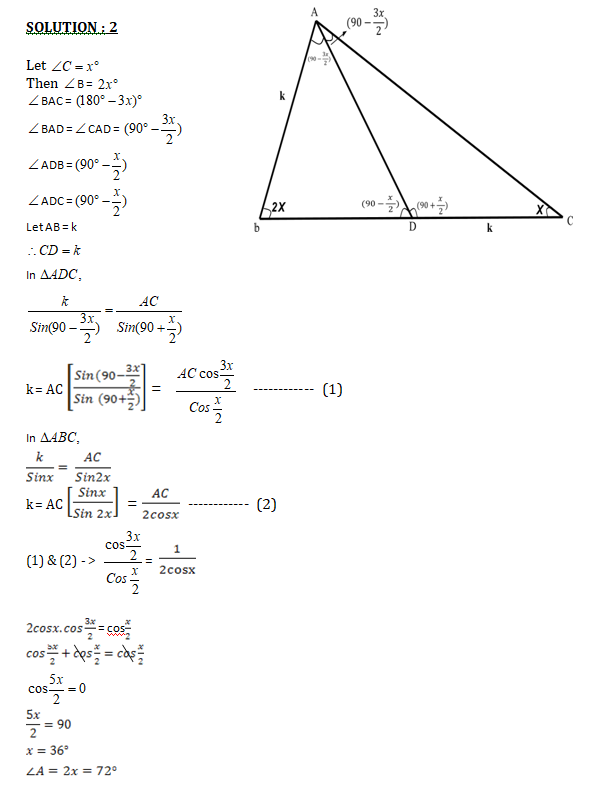
16. Question
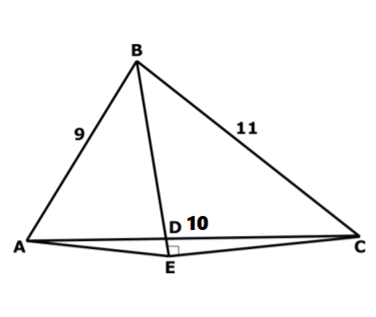
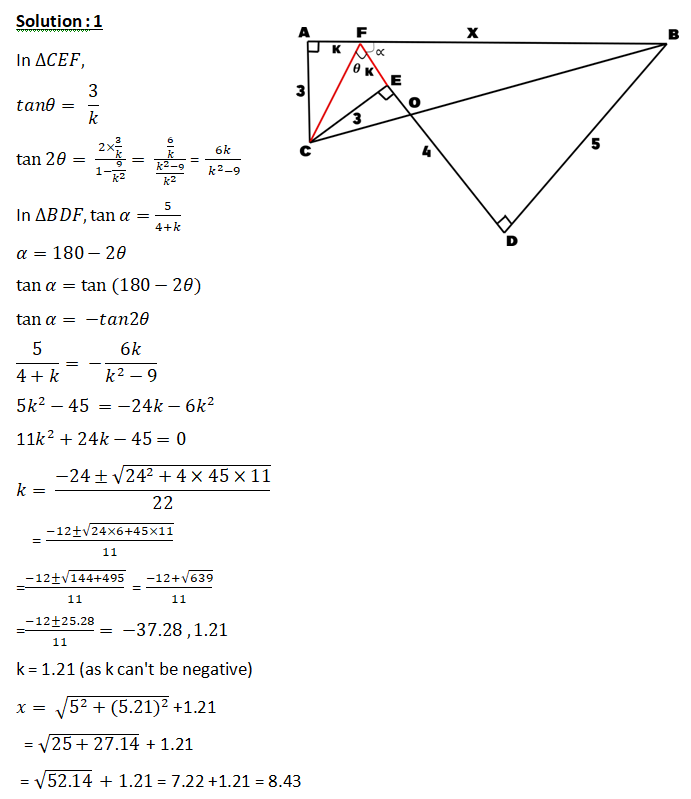
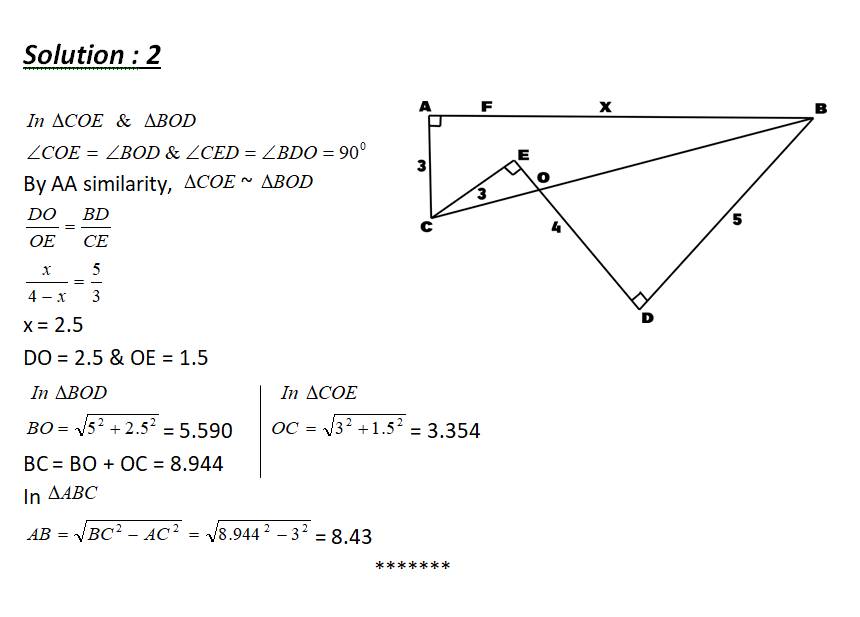
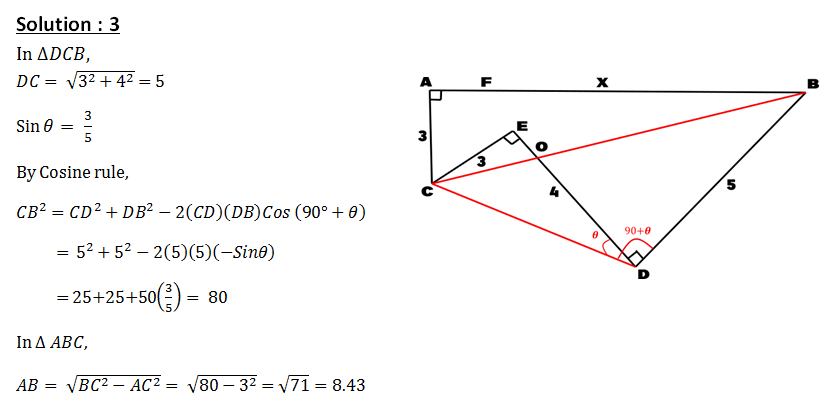
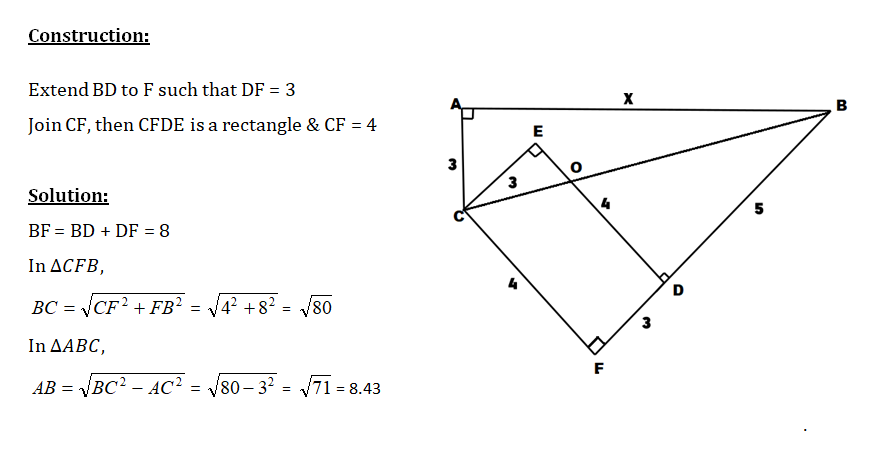
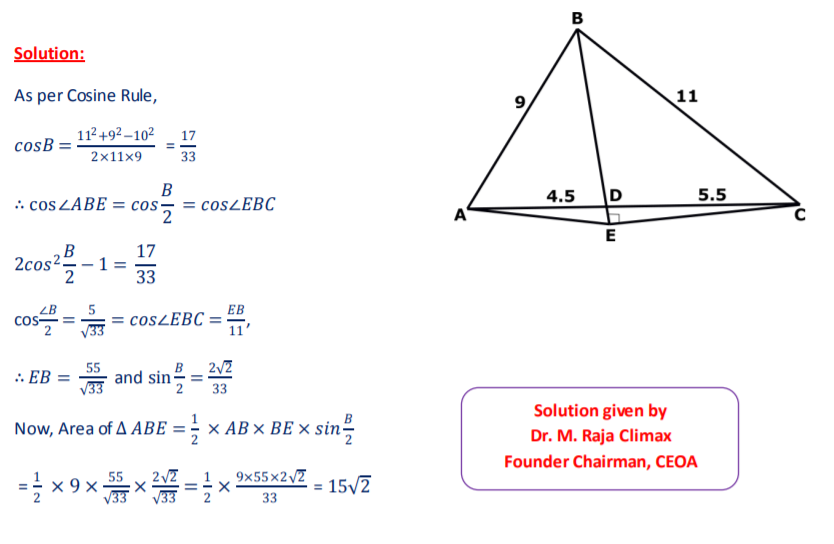
In ∆ 𝑨𝑩𝑪,𝑨𝑩 = 𝟗, 𝑨𝑪 = 𝟏𝟎 𝒂𝒏𝒅 𝑩𝑪 = 𝟏𝟏.Point D is on AC such that BD is an angle bisector, and E is on BD such that CE ⊥ 𝑩𝑫.Compute the area of ∆ 𝑨𝑩𝑬.
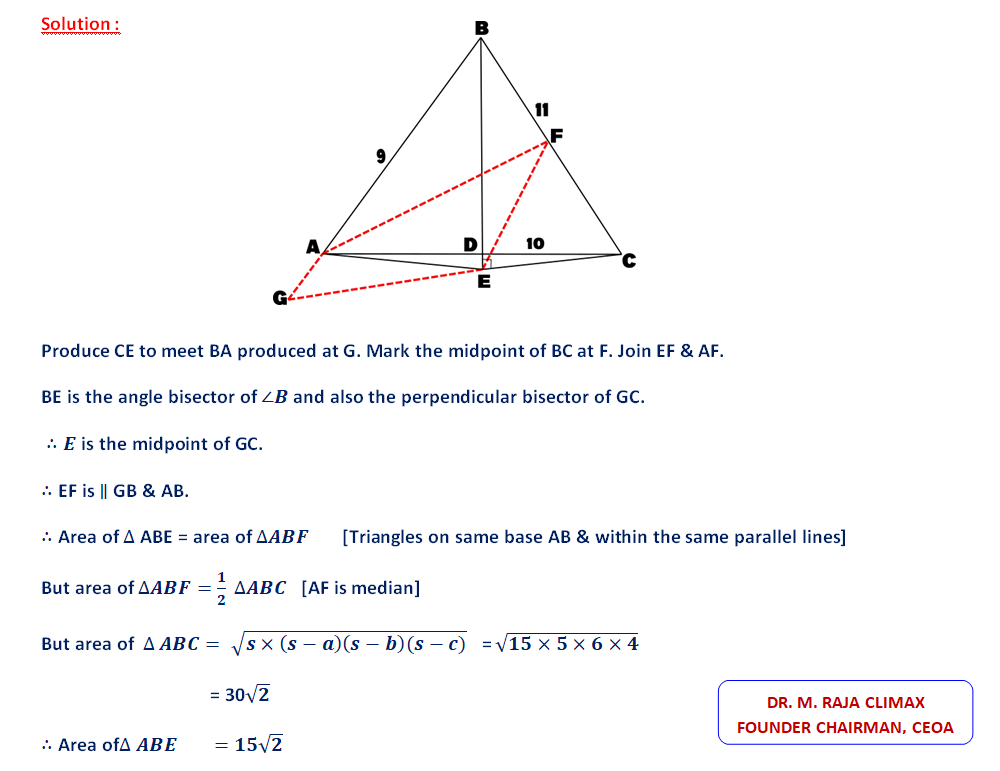
17. Author's Corollary
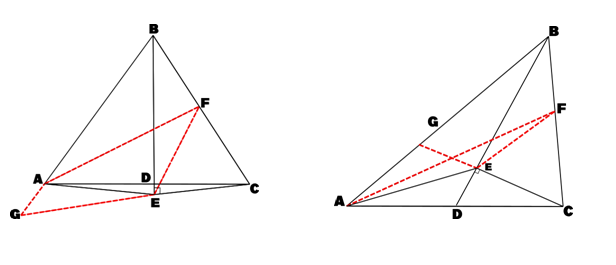
ABCis a Δ. BD is the bisector of ∠B meeting AC at D. CEis drawn ⊥ BD or BD produced. Prove that Area of Δ ABE = 1/2 area of Δ ABC
18. Question
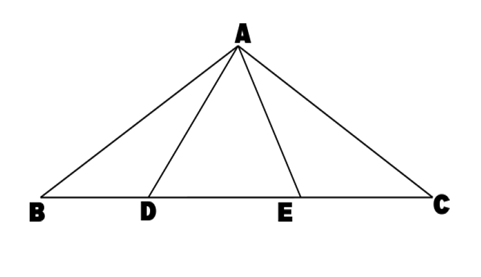
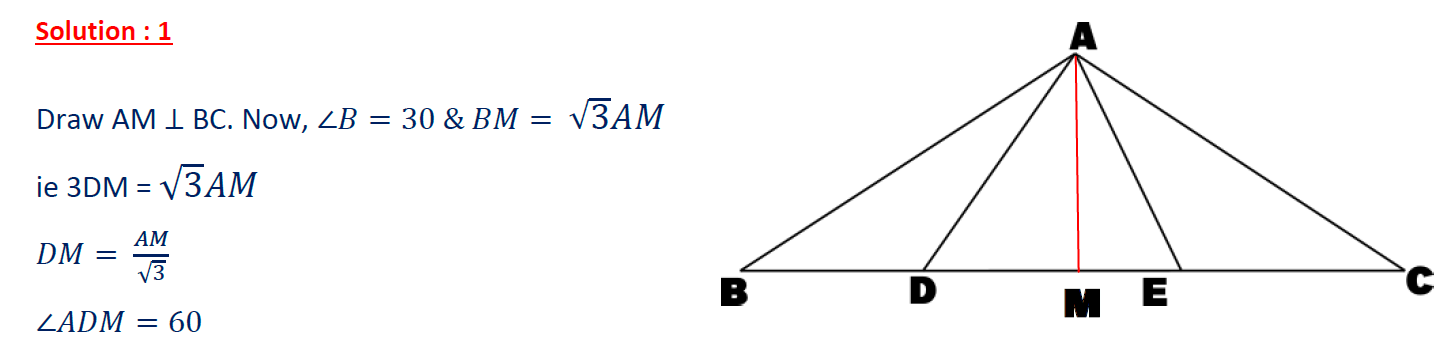
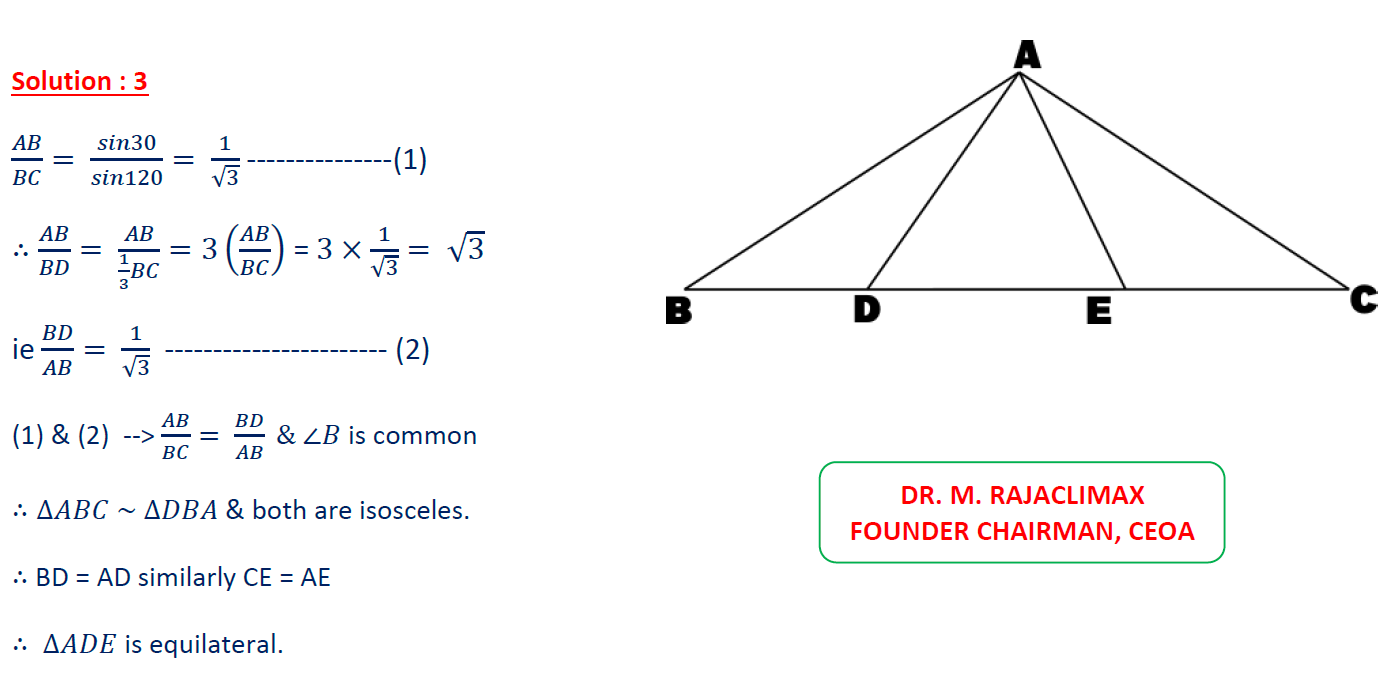
In triangle ΔABC, AB = AC and A = ∠120° . D,E are trisection points of BC. Prove that ΔADE is equilateral.