Quadrilaterals

Quadrilaterals
Cyclic Quadrilaterals
Author's Creation
Author's Solution

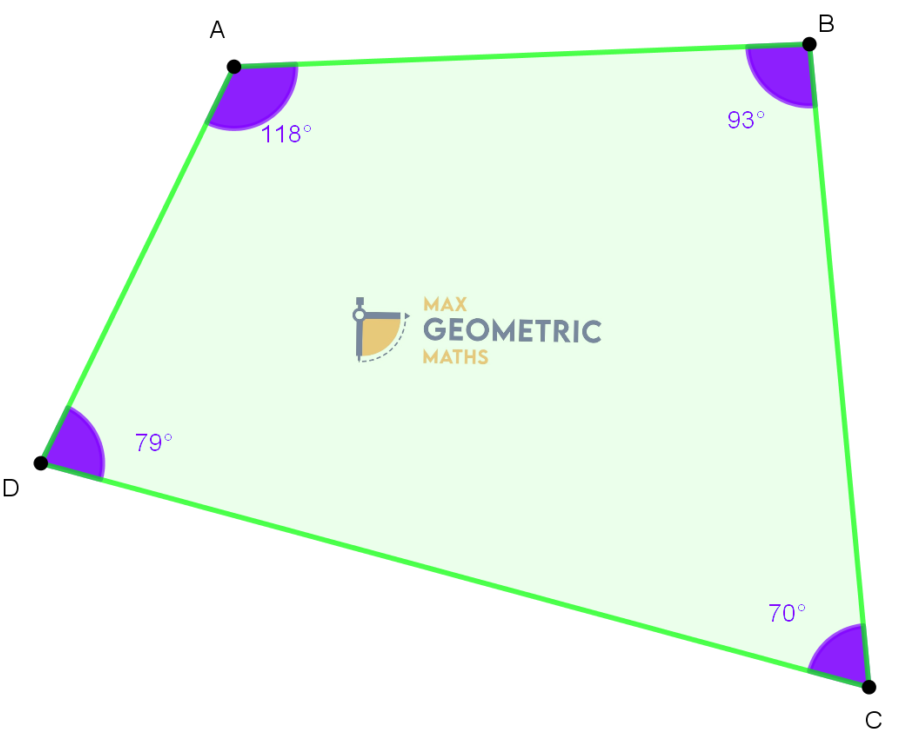
Ordinary Quadrilaterals

A quadrilateral is a two dimensional shape having four vertices & four sides.

Quadri (four) + Latus (Side) = Quadrilateral (four Sided figure)

Also known as Quadrangle or Tetragon.

Sum of the interior angles = 360⁰

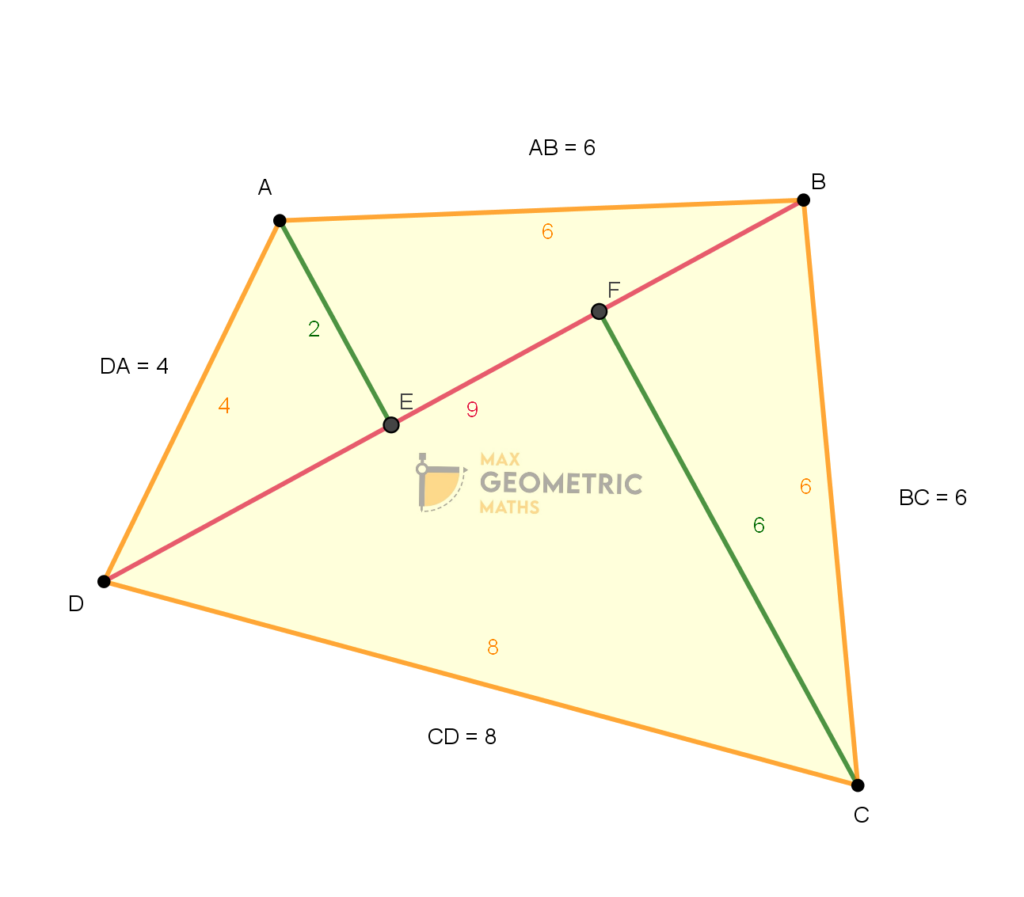
Area & Perimeter of the quadrilateral:

AREA

Area of the quadrilateral = ½ x diagonal x (sum of the perpendicular lengths

Area of the quadrilateral ABCD =(1/2) x 9 x (2+6) = 36 sq.cm

PERIMETER

Perimeter of the quadrilateral = sum of the sides of the quadrilateral.

Perimeter of the quadrilateral ABCD = 6 + 6 + 8 + 4 =24 cm

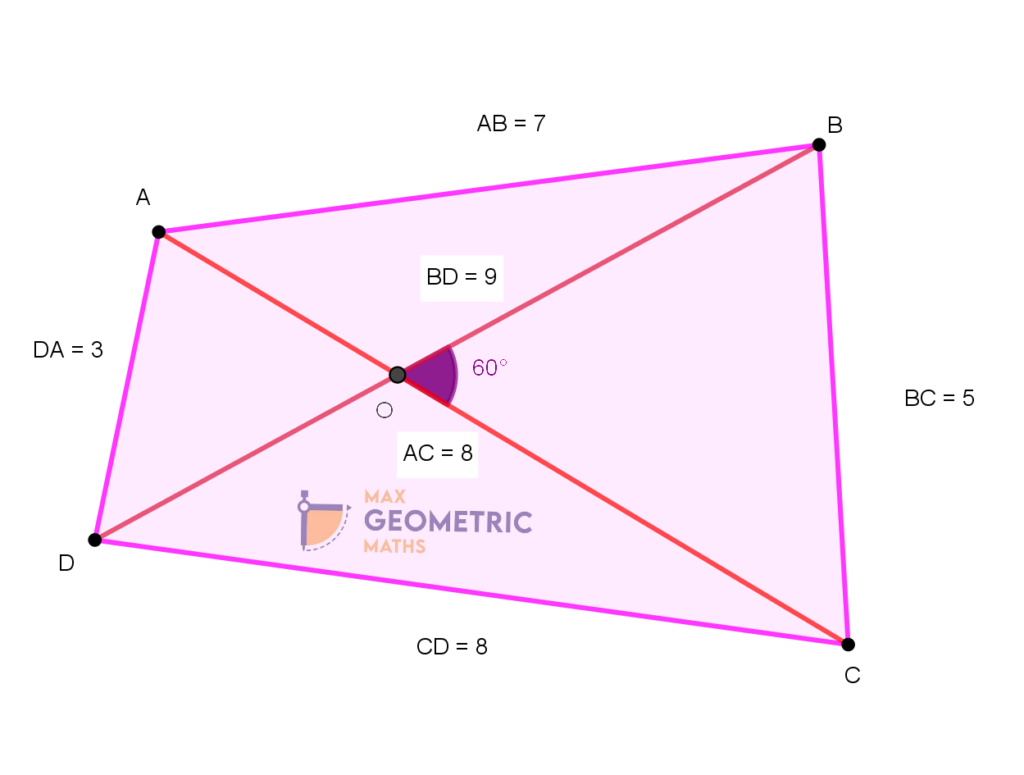
New Formula for finding the Area of a Quadrilateral:

Area of the quadrilateral = ½ x Product of diagonals x Sine of the angle between them.

Area of the quad ABCD = ½ x 9 x 8 x Sin 60⁰

= ½ x 9 x 8 x (√3/2)

= 18 sq.cm

Note: If the angle between the diagonals is 30º, then the formula is more simple

Area of the quad ABCD = (Product of the diagonals)/4

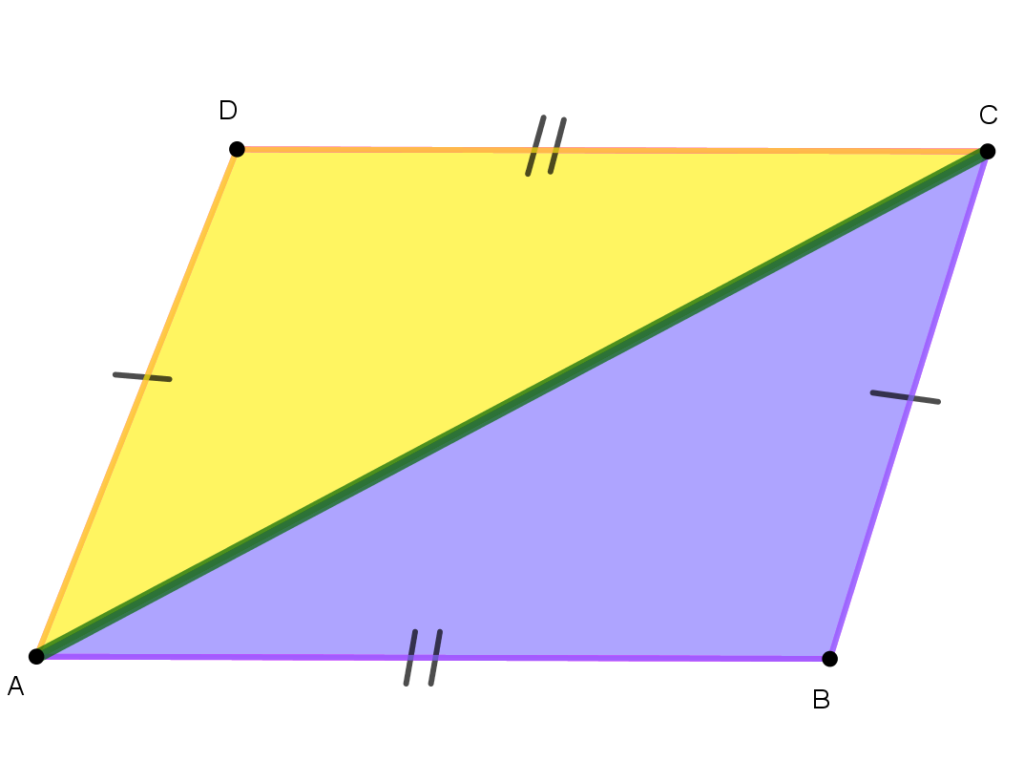
Parallelogram

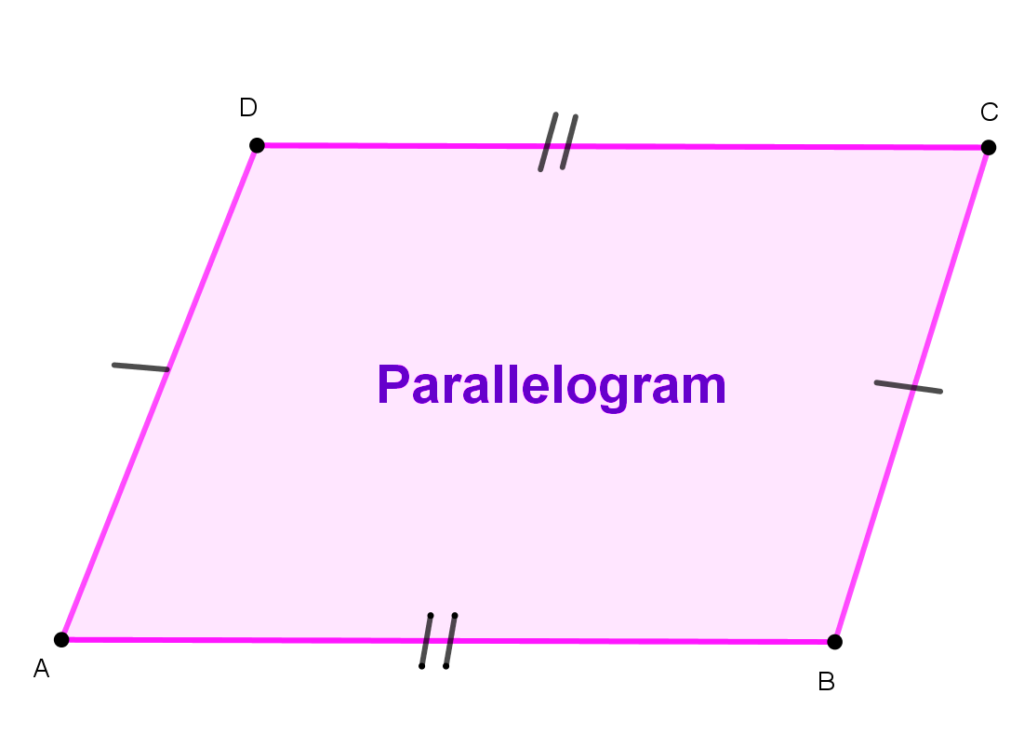
1. Opposites sides are equal & parallel
2. Opposite angles are equal
3. Consecutive angles are supplementary.
4. Diagonals that bisect each other.

Rectangle

1. Opposites sides are equal & Parallel
2. All angles are equal to 90°
3. Diagonals are equal & bisect each other.

Trapezium

Only one pair of opposite sides is parallel.

Isosceles Trapezium

1. Only one pair of opposite sides is parallel.
2. Non-parallel sides are equal.

Square

1. All sides are equal.
2. All angles are equal to 90°
3. Opposites sides are Parallel
4. Diagonals are equal & bisect each other at right angles.

Rhombus

1. All sides are equal.
2. Opposites sides are Parallel
3. Opposite angles are equal
4. Diagonals bisect each other at right angles.

Kite

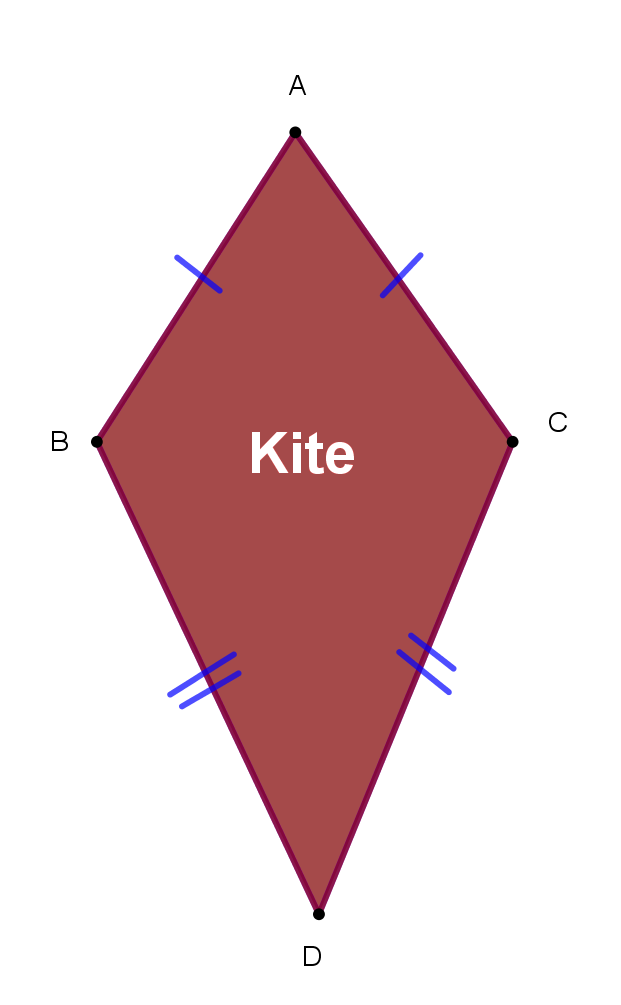
1. Two pairs of adjacent sides are equal.
2. One pair of opposite angles (that are obtuse) are equal
3. Diagonals are perpendicular to each other
4. The longer diagonal bisects the shorter diagonal.

Quadrilaterals	Dimensions	Area	Perimeter
Parallelogram	Breadth = b Height = h Length of parallel sides = a, b	b x h	2 (a + b)
Rectangle	Breadth = b	l x b	2 ( l + b)
Square	Side = a	a²	4a
Rhombus	Length of the diagonals = d₁ , d₂	½ x d₁ x d₂	4a
Trapezium	Length of Parallel Sides = a, b. Height = Distance between parallel sides = h	½ x ( a + b) x h	Sum of all sides
Kite	Length of the diagonals = d_1,d₂ Length of adjacent sides = a, b.	½ x d₁ x d₂	2 (a +b)

Theorems

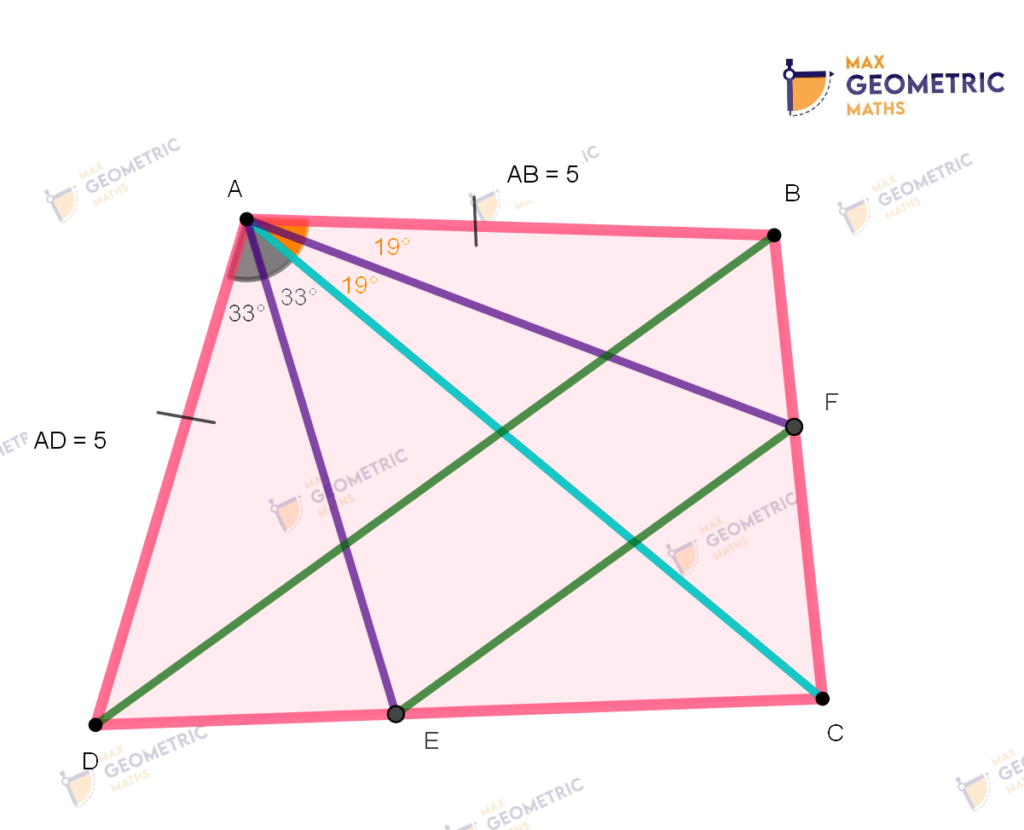
Theorem # 1

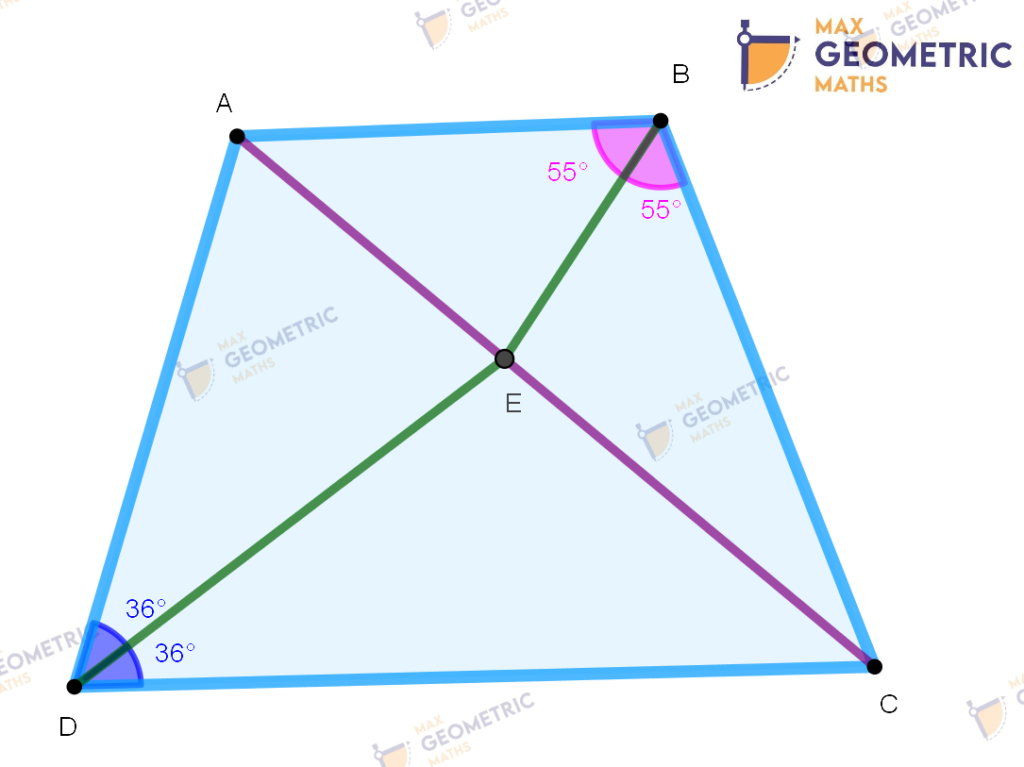
A diagonal of a parallelogram divides it into two congruent triangles.

Theorem # 2

ABCD is a quadrilateral with AB=AD. If AE & AF are internal bisectors of ∠DAC & ∠BAC respectively, then EF is parallel to BD.

Theorem # 3

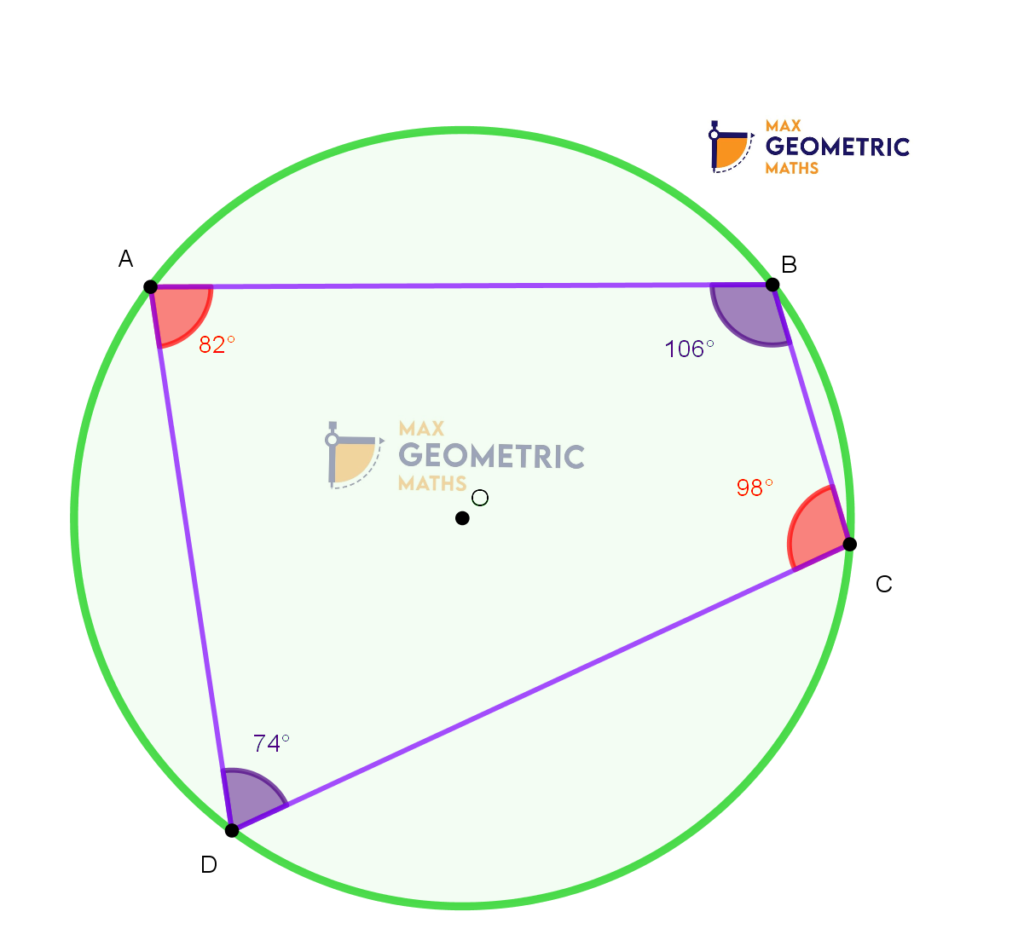
In a quadrilateral ABCD, if the bisectors of B & D intersect on AC at E, then AB/BC = AD/DC

Cyclic Quadrilaterals

A quadrilateral is called Cyclic quadrilateral if its all vertices lie on the circumference of a circle.

If ABCD is a cyclic quadrilateral, then the points A,B,C,D are called as concyclic points.

Theorem # 1

The sum of the opposite angles of a cyclic quadrilateral is supplementary. ∠A + ∠C = 180º ∠B + ∠D = 180º

Theorem # 2

In a cyclic quadrilateral, the four perpendicular bisectors of the given four sides meet at the centre O.

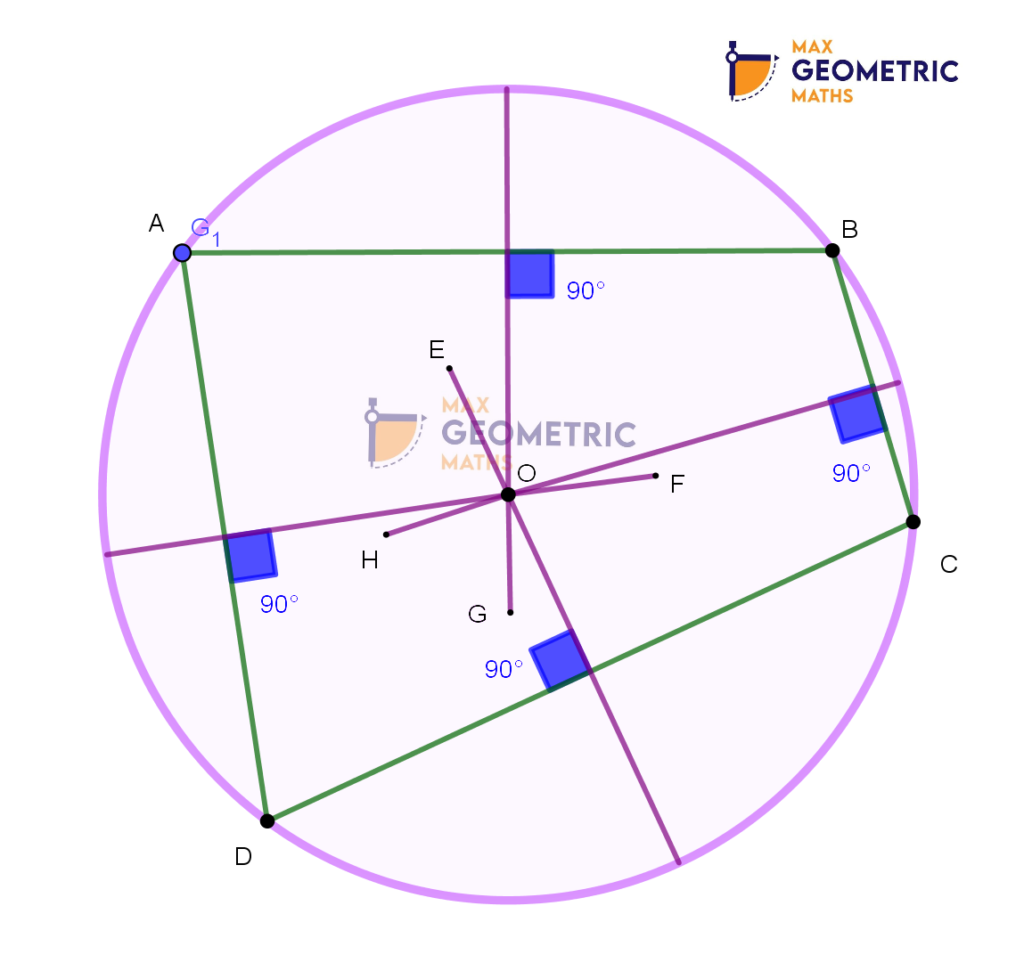
Theorem # 3

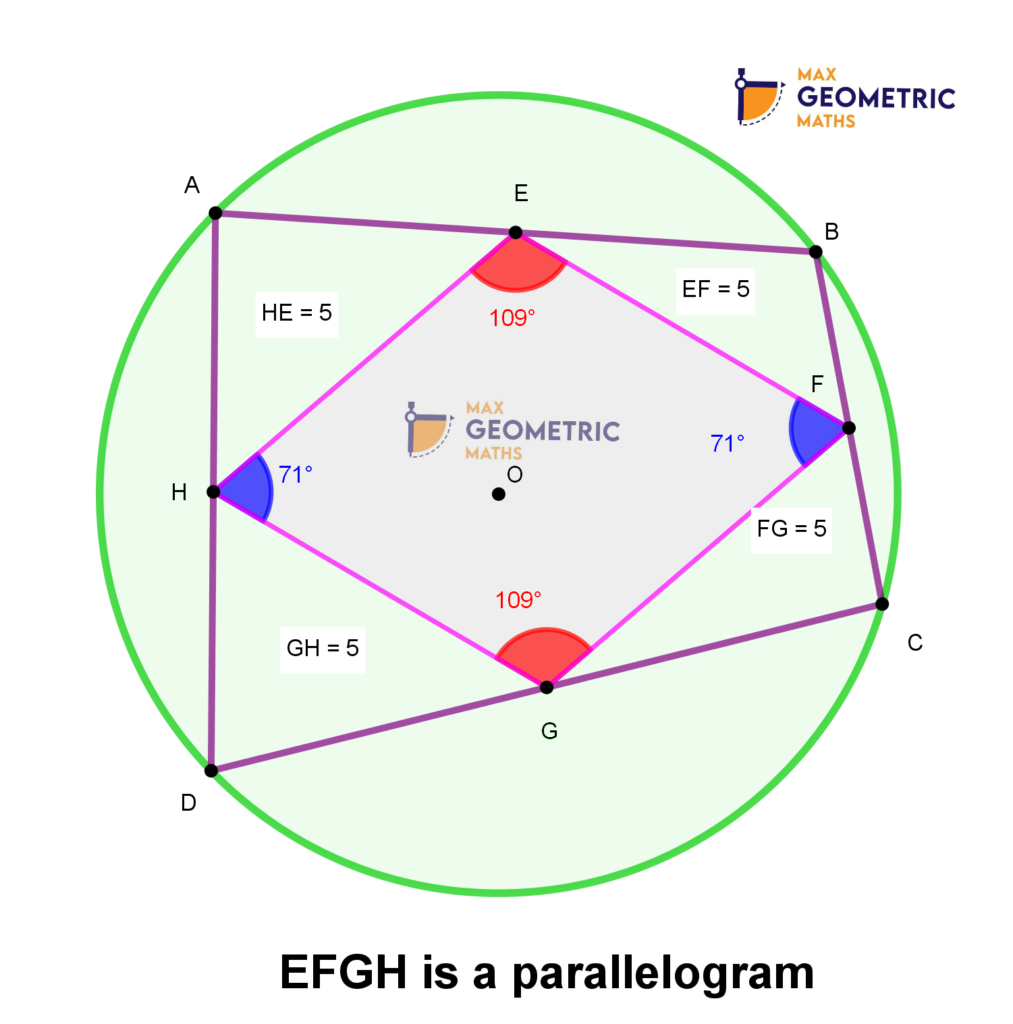
When the midpoints of a cyclic quadrilateral are joined, it forms a parallelogram.

Theorem # 4

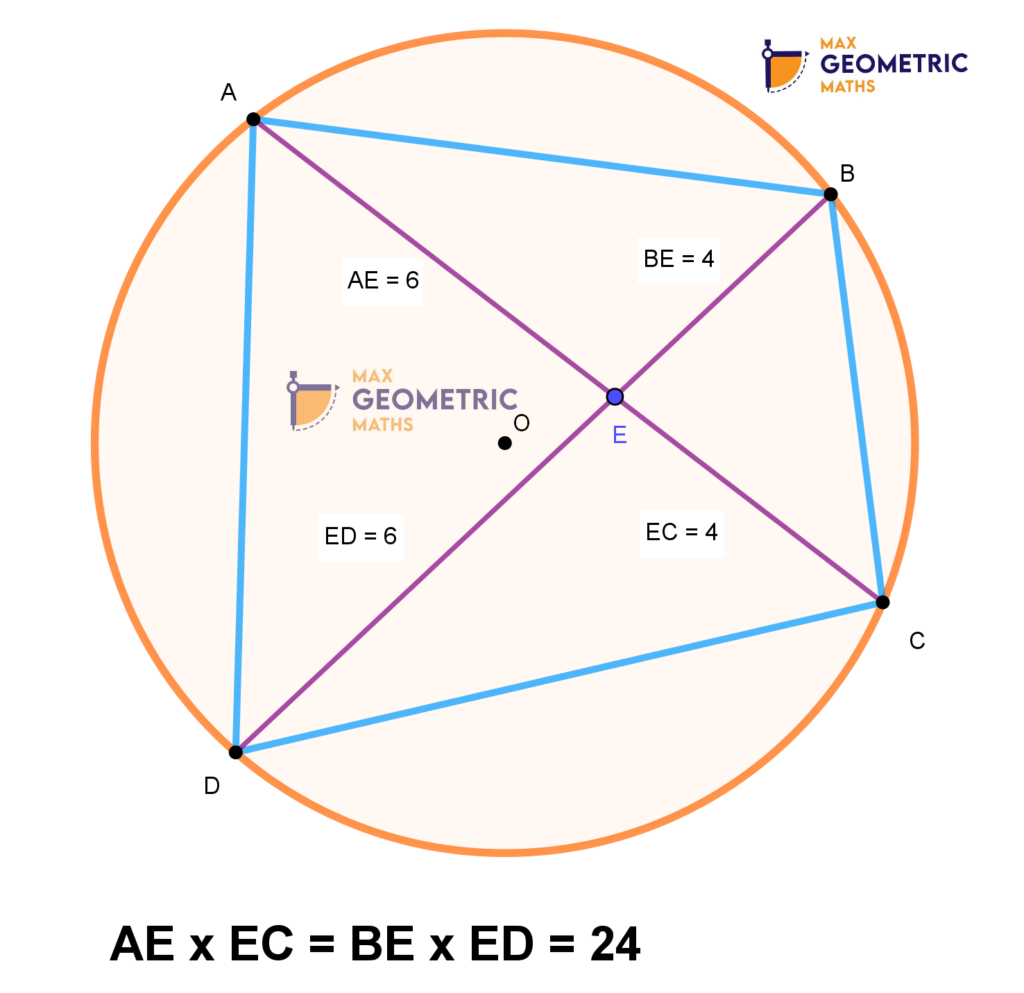
If E is the point of intersection of the two diagonals, AE x EC = BE x ED.

Theorem # 5

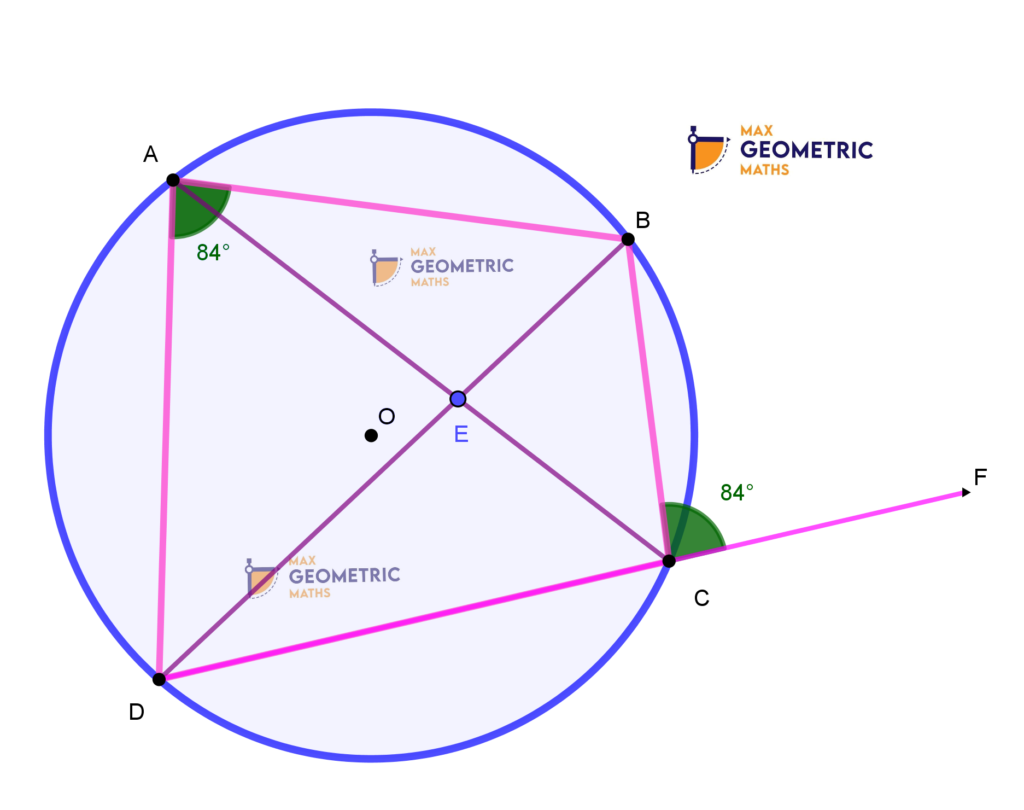
The exterior angle formed if any one side of the cyclic quadrilateral produced is equal to the interior angle opposite to it.

Theorem # 6

1. For a parallelogram to be cyclic or inscribed in a circle, the opposite angles of that parallelogram should be supplementary.
2. A cyclic square/rectangle can be formed by taking the centre as the point of intersection of diagonals.

Theorem # 7

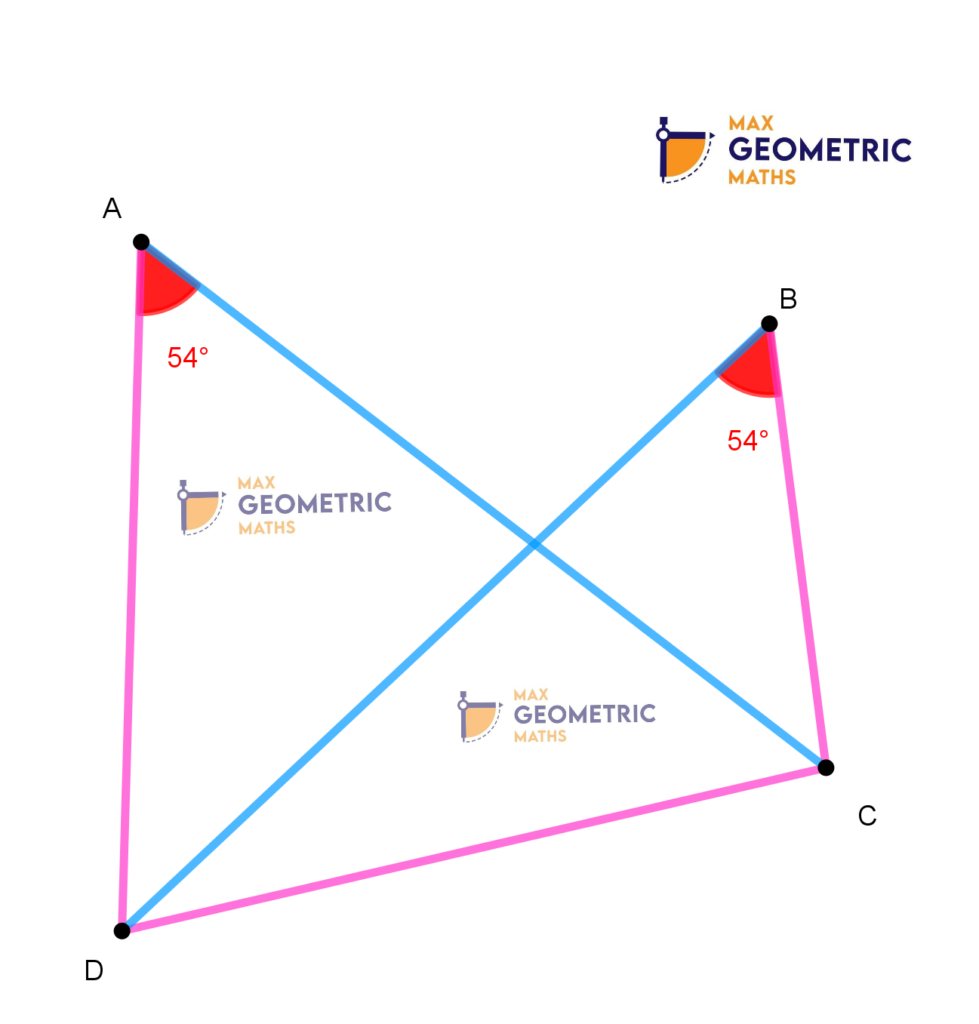
If the line segment joining two points subtends equal angles at two other points on the same side of the segment, then the four points are concyclic. Here, CD is the line segment subtending equal angles at A & B on the same side of CD, i.e., ∠DAC = ∠DBC,
Hence, Points A, B, C, D are concyclic.

Theorem # 8

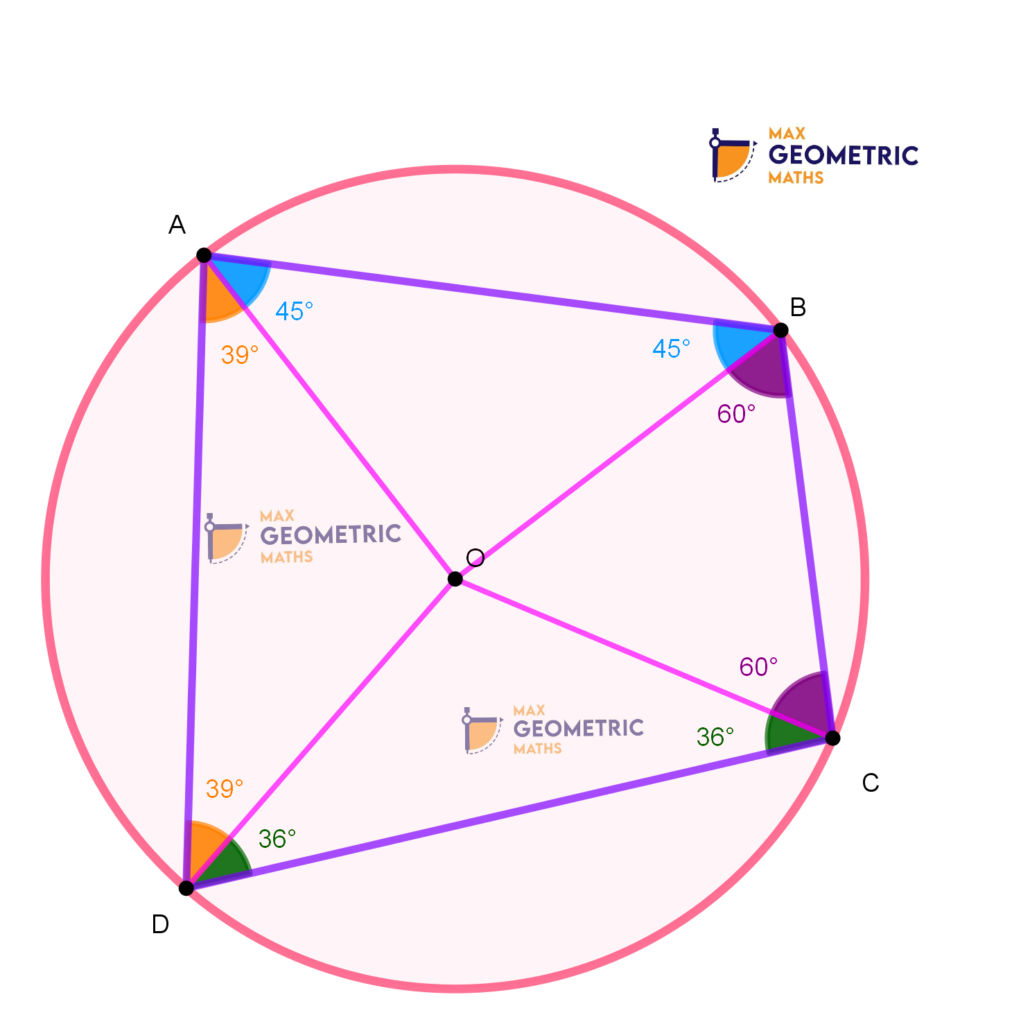
Joining the centre ‘O’ to the vertices A,B,C,D gives four isosceles triangles ΔOAB, ΔOBC, ΔOCD, ΔODA.

Ptolemy’s Theorem

The product of the diagonals is equal to the sum of the product of its two pairs of opposite sides.

If ABCD is a cyclic quadrilateral with AC & BD as diagonals, then (AB x CD) + ( BC x AD) = AC x BD

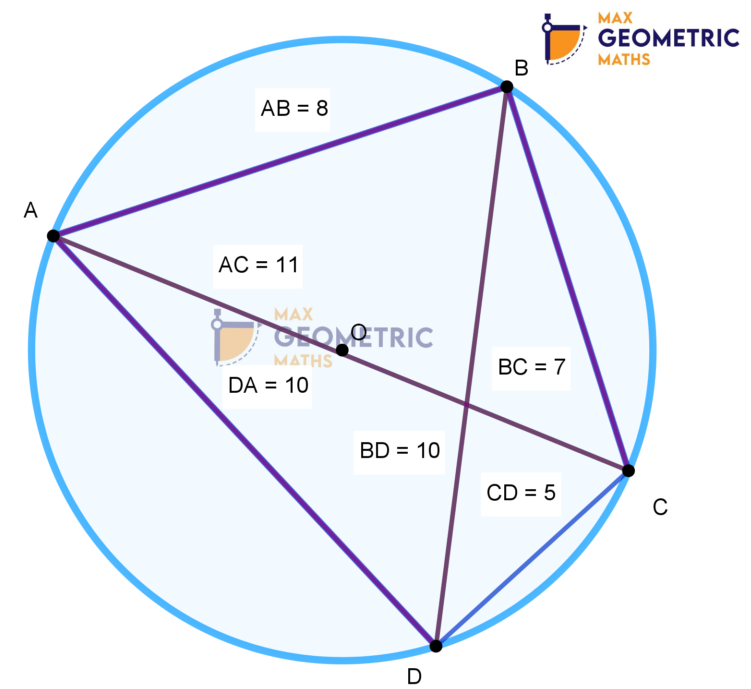
AC x BD = 11x10 = 110
(AB x CD) + (BC x AD)= (8 x 5) + (7 x 10) = 110

Brahmagupta Formula

(for finding Area of Cyclic Quadrilateral
Ifa, b, cand dare the sides of a cyclic quadrilateral, then its area is given by:

Where s is the semi perimeter s = 1/2(a+b+c+d)

Diagonals of Cyclic Quadrilaterals

Suppose a, b, c and d are the sides of a cyclic quadrilateral and di & d2 are the diagonals, then we can find the diagonals of it using the below given formulas:

Radius of Cyclic Quadrilateral

(for finding Area of Cyclic Quadrilateral
Ifa, b, cand dare the sides of a cyclic quadrilateral, then its area is given by:

Where s is the semi perimeter s = 1/2(a+b+c+d)

Brahmagupta’s theorem

In a cyclic quadrilateral if the diagonals intersect each other at right angles, then the perpendicular to a side from the point of intersection of the diagonals always bisects the opposite side.

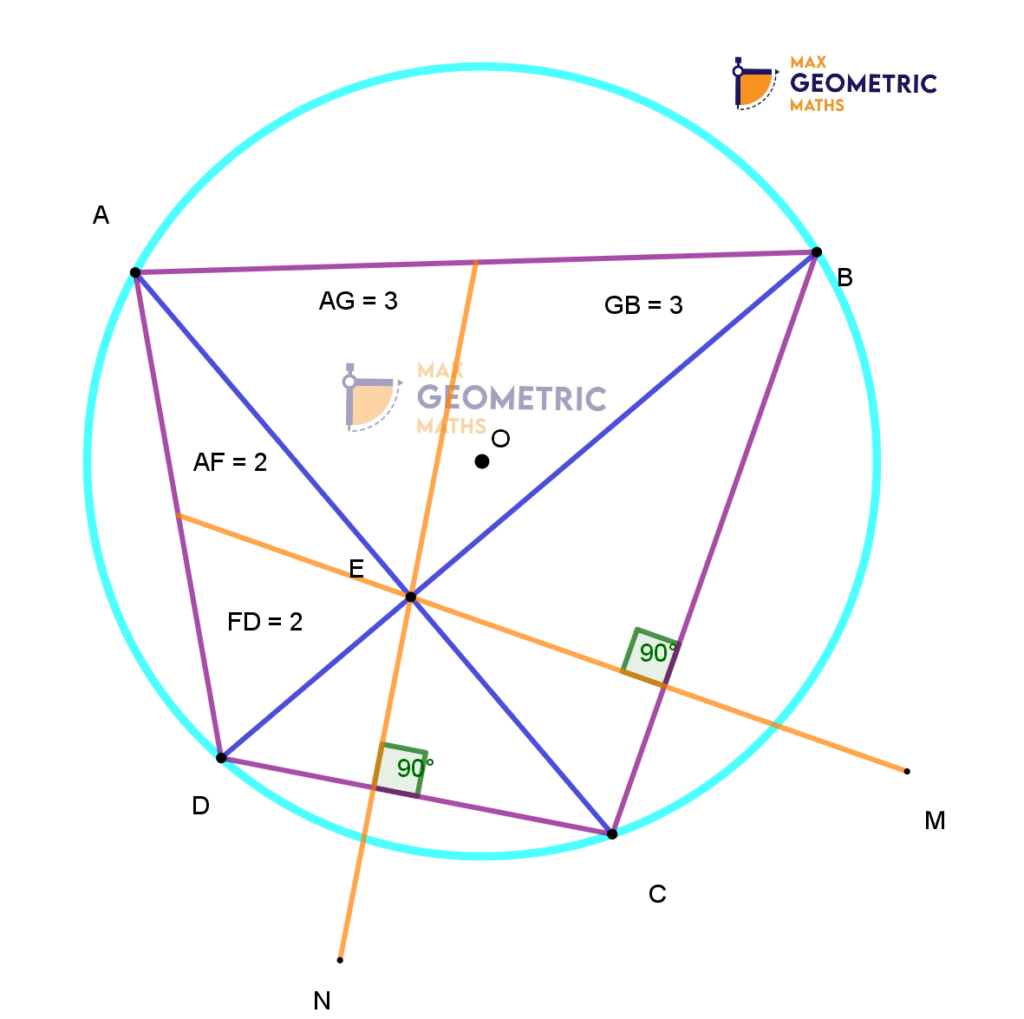
Author’s Creation in Quadrilaterals

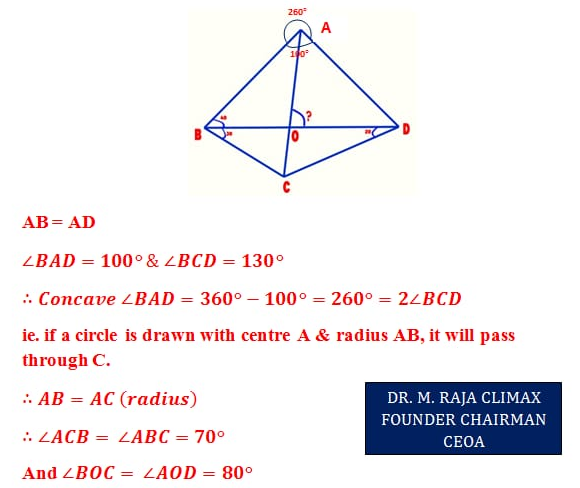
1. Question:

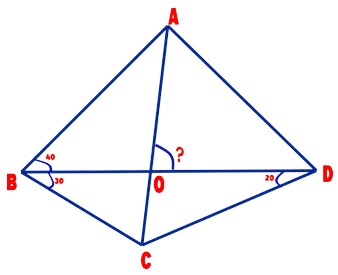
In quadrilateral ABCD, AC & BD meet at O; AB = AD; ∠ABD = 40°; ∠CBD = 30°; and ∠BDC = 20°. Find the measurement of ∠AOD.

Question created by
Dr.M.Raja Climax Founder Chairman, CEOA

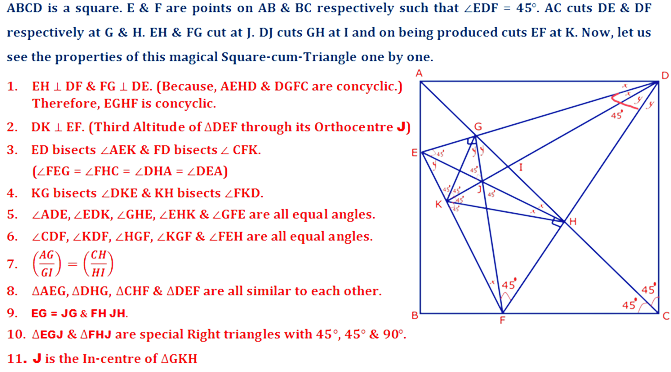
2. Question:

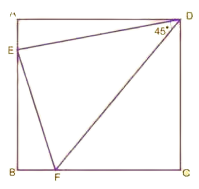
ABCD is a square. E & F are points on AB & BC respectively such that ∠EDF=45º. Prove that ED & FD are the bisectors of ∠AEF & ∠CFE

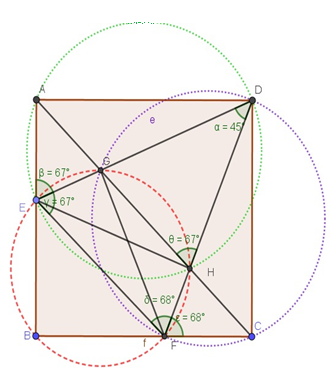
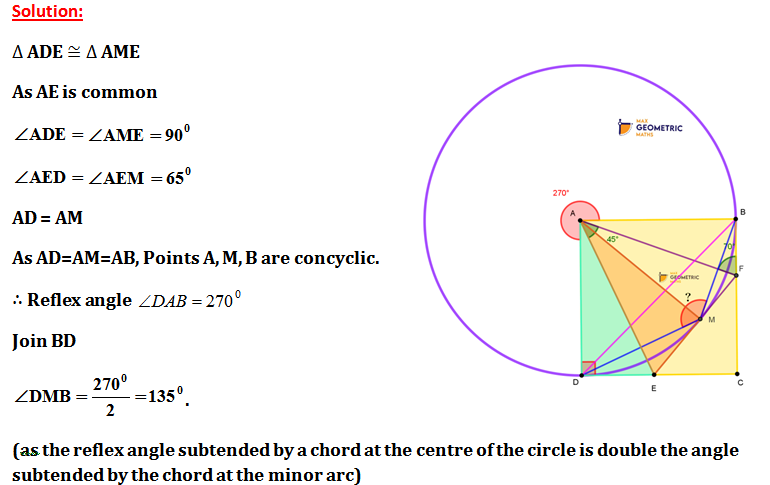
3. Question:

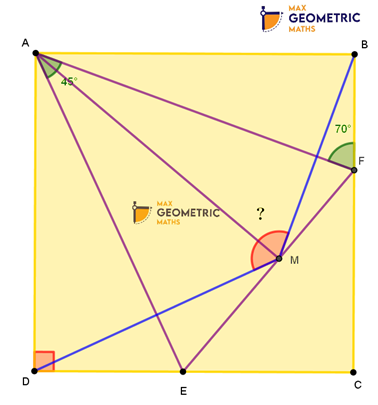
ABCD is a square. E & F are points on DC& BD respectively such that ∠EAF =45°& ∠AFB =70° as shown in the figure. Ifa perpendicular is drawn from Ato EF meeting EF at M, then find ∠DMB

4. Question:

Research done by
Dr.M.Raja Climax
Prof G. LAKSHMANA MURTHY.

5. Question:

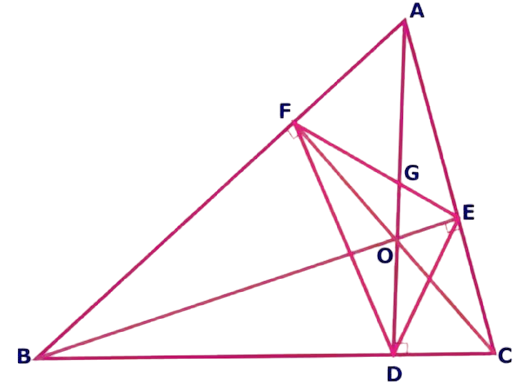
In the above figure, ‘O’ is the orthocentre of Δ ABC. Identify & write the cyclic quadrilaterals figuring inside ΔABC.

6. Question:

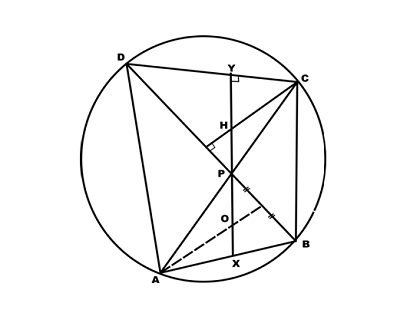
Modified Rider :

The diagonals AC and BD of a cyclic quadrilateral ABCD intersect at P. Let O be the centroid of ∆APB and H be the orthocentre of ∆CPD. Show that the points H,P,O are collinear.

7. Question:

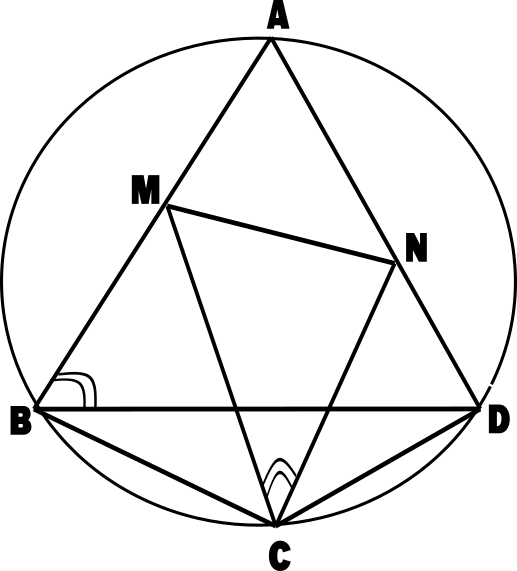
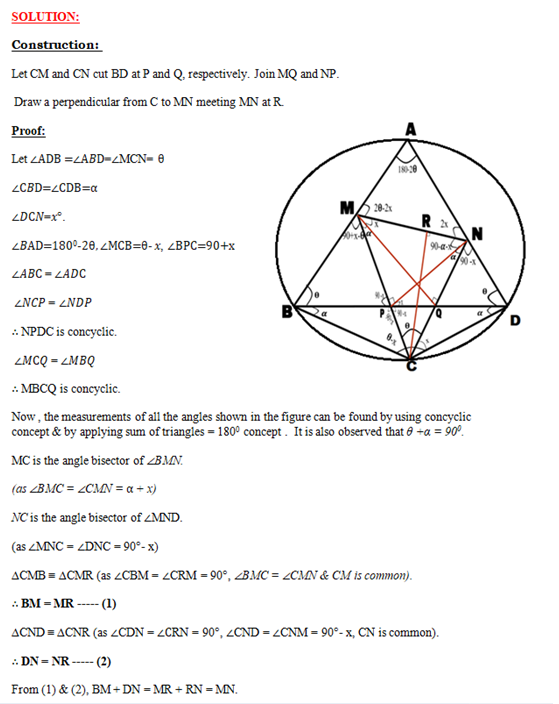
ABCD is a Cyclic quadrilateral with AB = AD and CB = CD. M and N are points on AB and AD respectively such that ∠MCN = ∠ABD. Prove that MN = MB + ND.

8. Question:

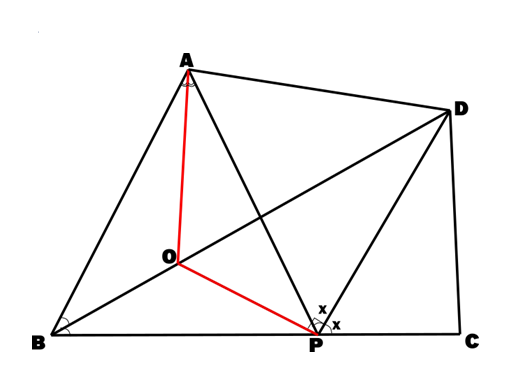
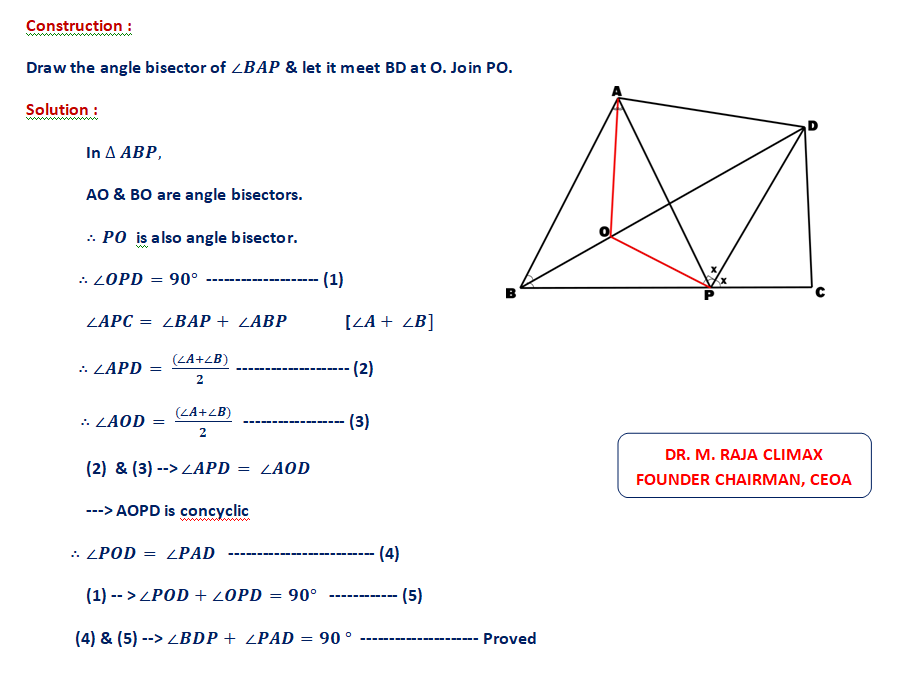
Given a quadrilateral ABCD where BD bisects ∠B , P is a point on BC such that PD bisects ∠APC. Show that ∠BDP + ∠PAD = 90°

Click here to view the problem in GeoGebra.

https://www.geogebra.org/m/yanv3fgj

Author’s Solution for Challenging Problems in Quadrilaterals

1. Question:

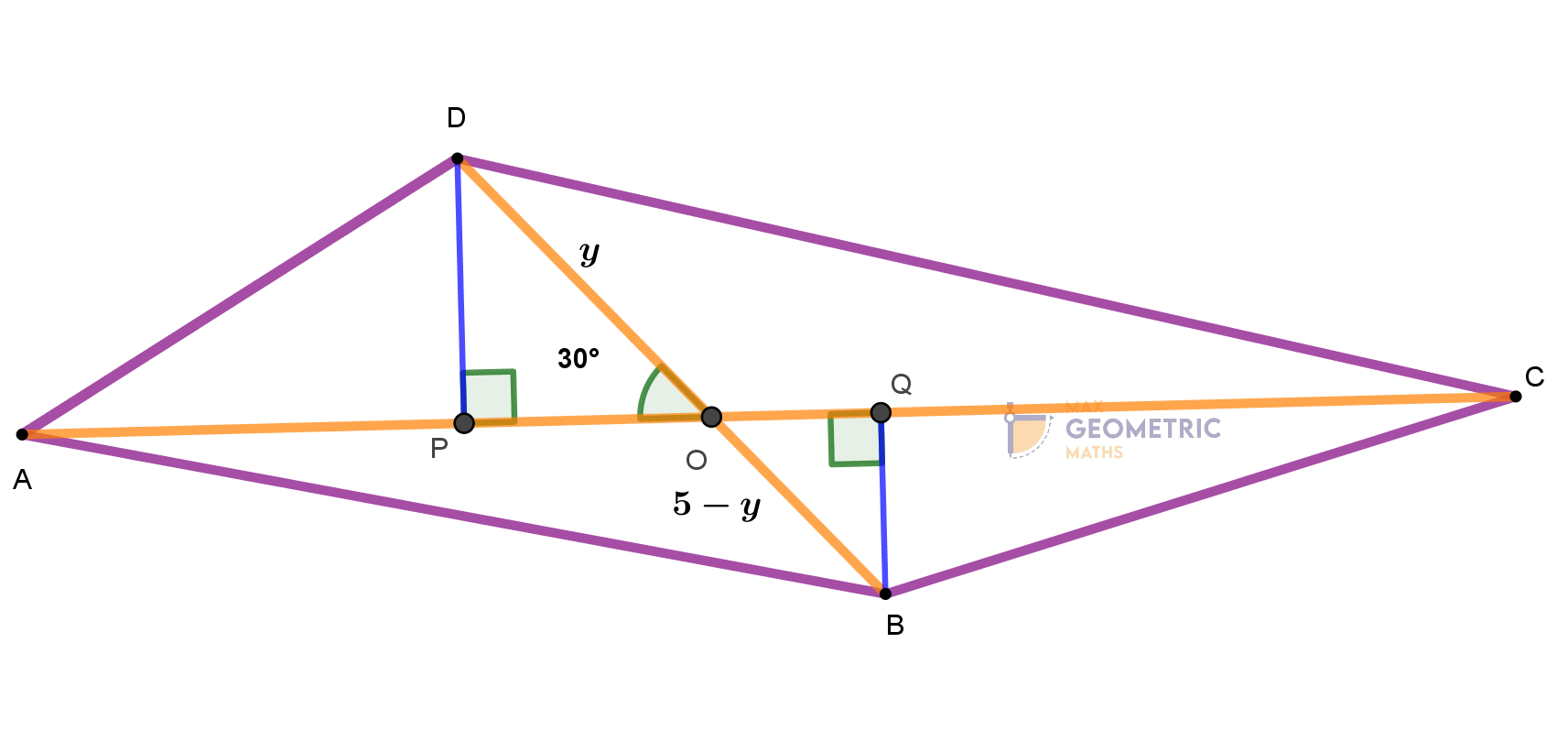
ABCD is a quadrilateral. Its diagonals AC & BD measuring 6 cm & 5 cm respectively cut each other at O and ∠AOD is 30°. Find the area of the quadrilateral ABCD.

Question created by
Dr.M.Raja Climax Founder Chairman, CEOA

2. Question:

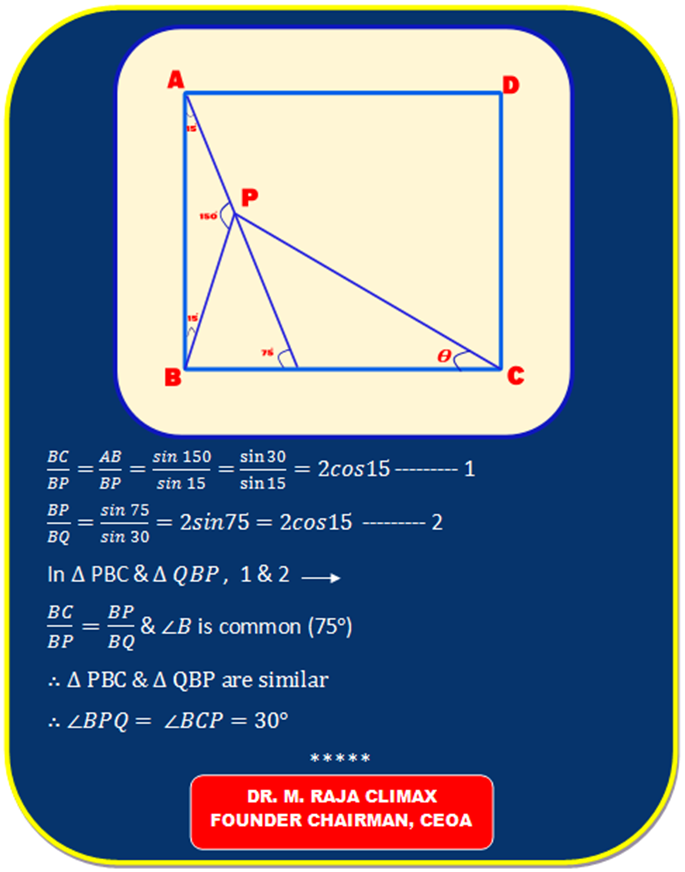
Find the value of θ, if ∠PAB = ∠ PBA = 15º

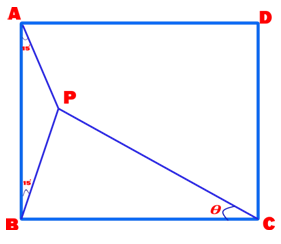
The question sender was taken aback on viewing two simple solutions for such a challenging problem.

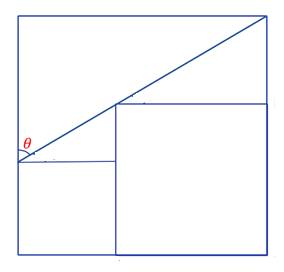
3. Question:

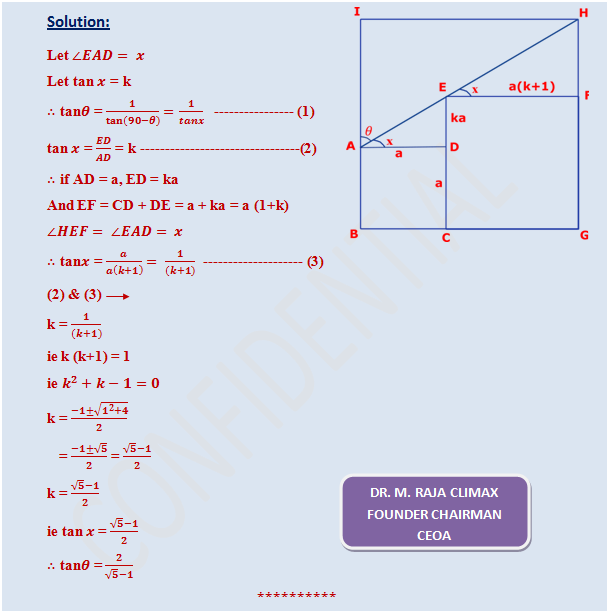
Find tanθ in the given figure

4. Question:

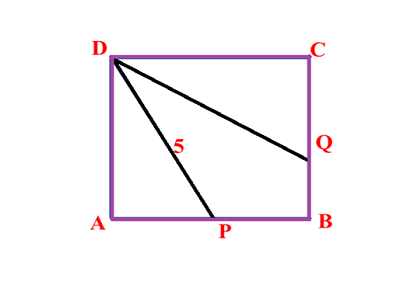
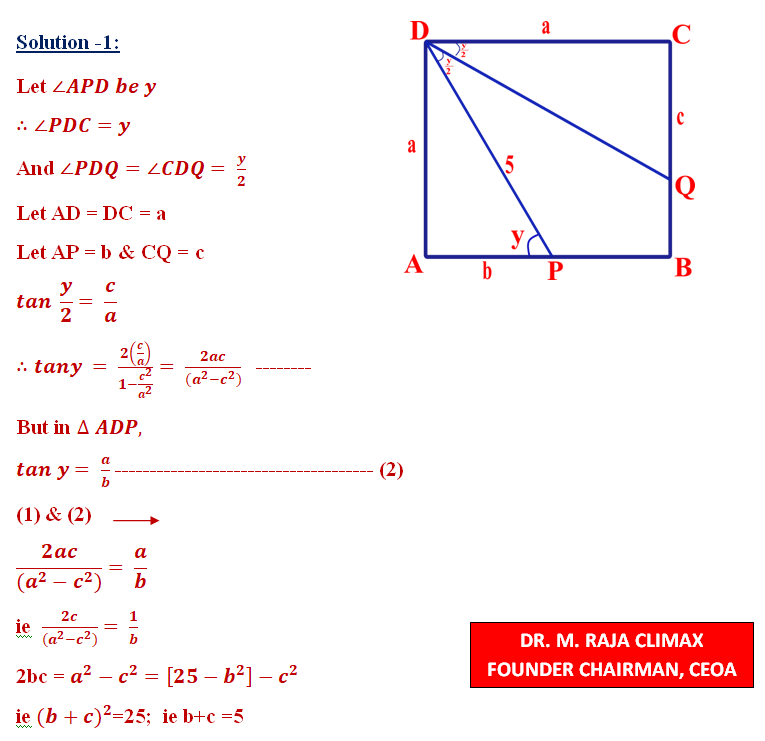
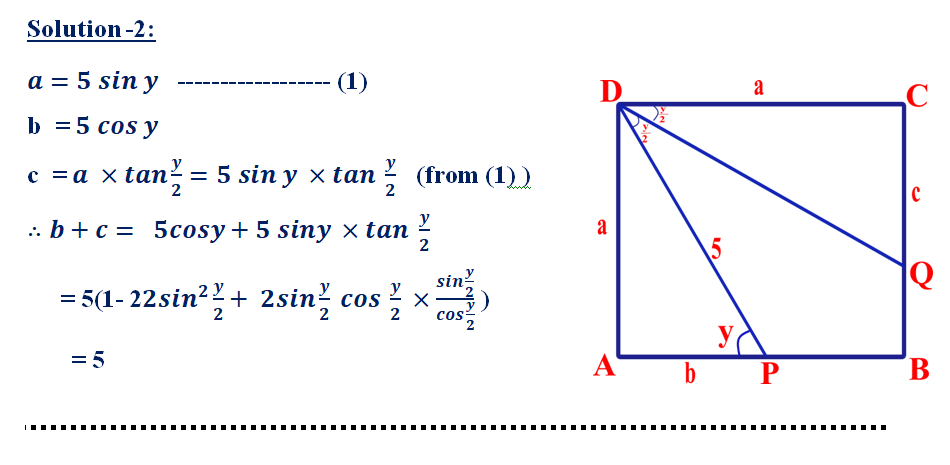
P is a point on side AB of square ABCD such that DP =5cm. DQ is the angle bisector of ∠PDC where Q is a point on side BC. Then find the length of (CQ+AP)

5. Question:

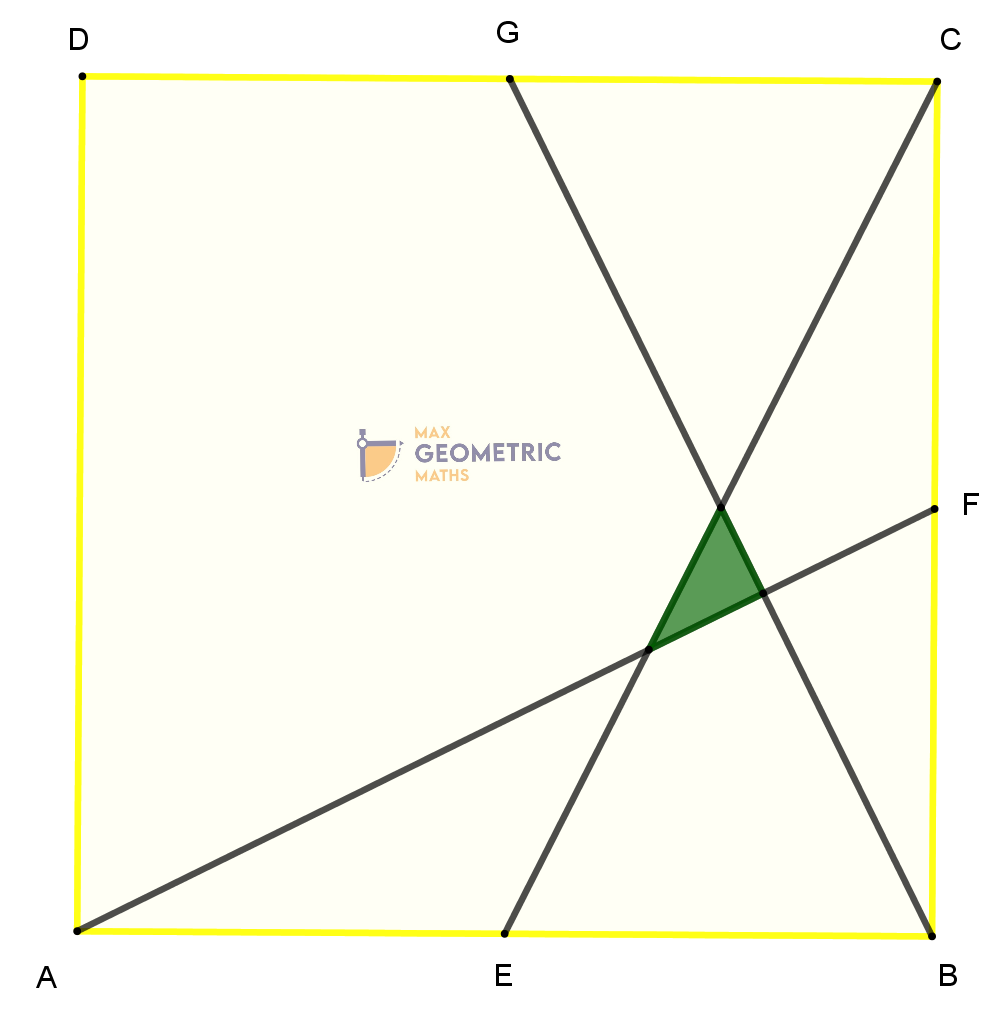
If ABCD is a square with side 5 cm, E, F, G are the midpoints of the sides AB, BC, CD respectively. Find the area of the shaded region

6. Question:

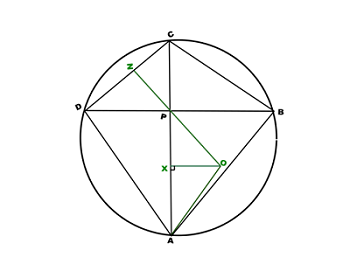
ABCD is a cyclic quadrilateral. AC & BD meet at P. O is the circumcentre of ∆ APB. Prove that, PZ is an altitude of ∆ CPD and there by prove that O, P and the orthocentre of ∆CPD are collinear,

7. Question:

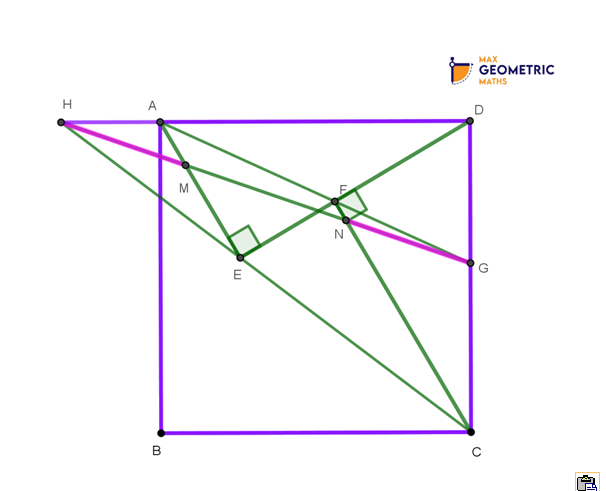
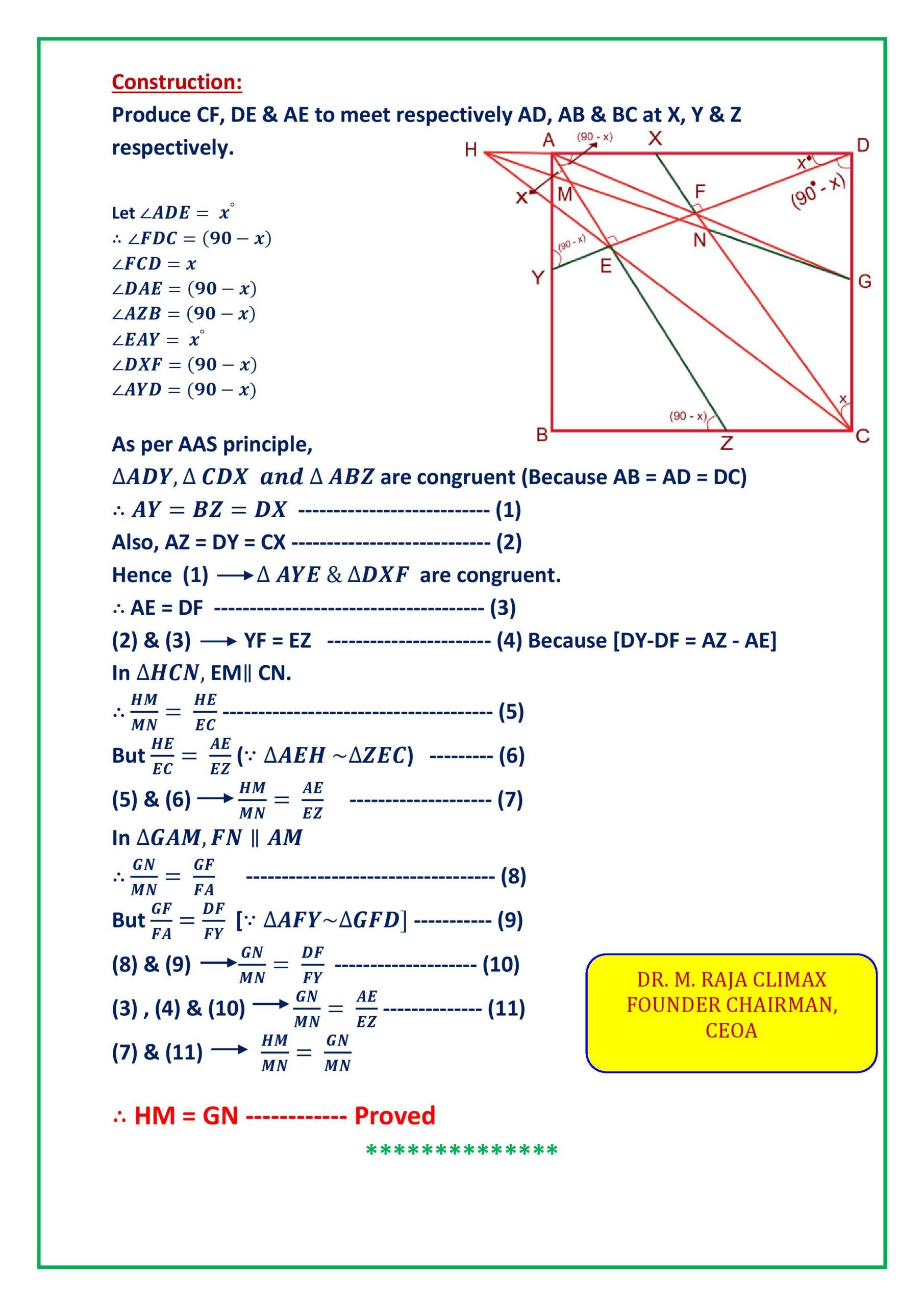
In the square ABCD, E is the interior point such that ∠AED is 90º. F is point on DE such that ∠CFD is 90º. AF meets CD at G. CE meets DA at H. Lines GH and CF meets at N, GH and AE meet at M. Then prove that GN=HM

8. Question:

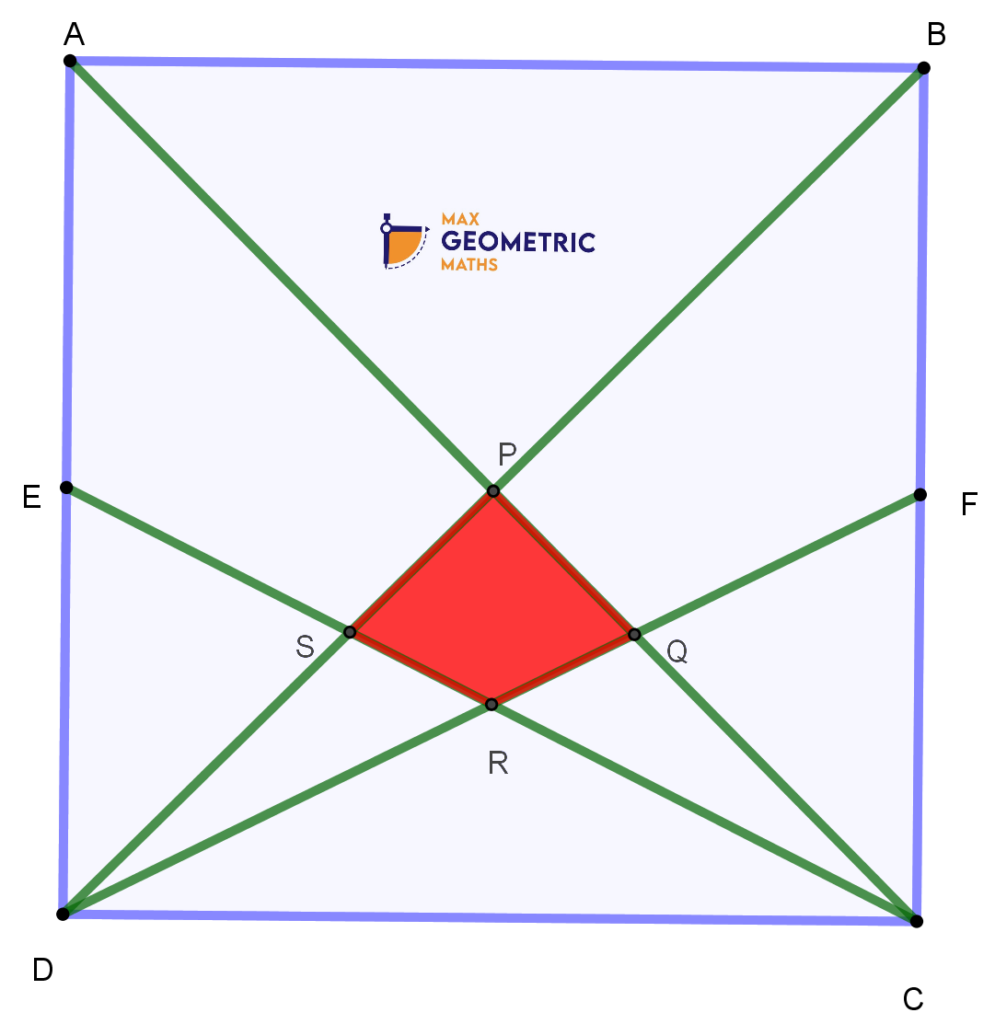
ABCD is a square. E & F are mid-points of sides AD & BC respectively. Line segments AC,BD,CE & DF intersect in the interior of the square to form a quadrilateral PQRS as shown in the figure. What is the ratio of area PQRS to that of ABCD?

Quadrilaterals

Ordinary Quadrilaterals

Area & Perimeter of the quadrilateral:

New Formula for finding the Area of a Quadrilateral: