Circles
A circle is the locus of a point that maintains a constant distance with a fixed point (called as centre) and the fixed point is called as radius of the circle.
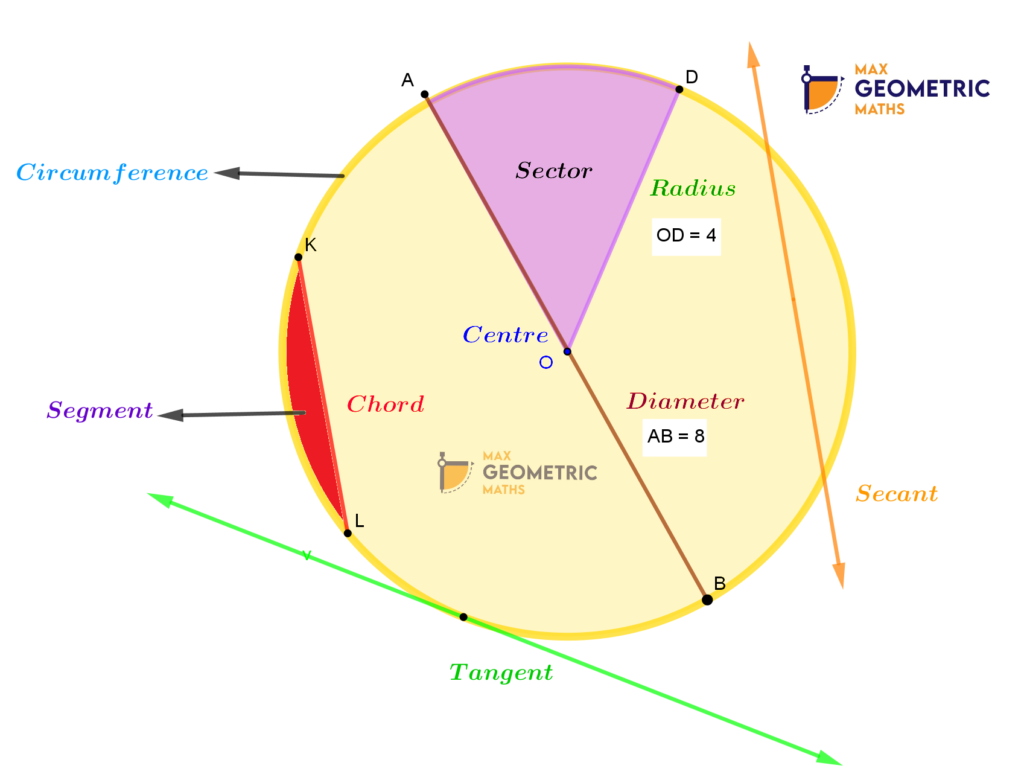
Chord: A line segment whose endpoints lie on the circle.
Diameter: The Chord passing through the centre of the circle. (It is the longest chord of the circle)
Radius: A line segment connecting the centre of a circle to any point on the circle.
Secant: A straight line cutting the circle at two points. It is also called an extended chord.
Tangent: A straight line touching the circle at any point.
Arc: The connected curve of a circle.
Sector: A region bounded by two radii and an arc.
Segment: A region bounded by two chords and an arc lying between the chord’s endpoints.
Circumference of the circle = The boundary of the circle = πd = 2πr units
Area of the circle = Space occupied by the circle = πr² Sq.units.
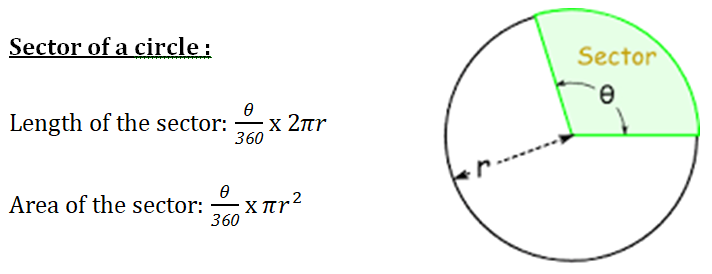
Types of Circles:
Concentric Circles
Same Centre but different radii.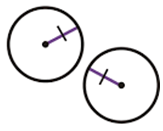
Congruent Circles
Different Centre but Same radii.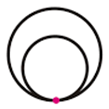
Tangent Circles
Two or more circles at a common point.Angles in Circles
Some Standard Results
Theorem # 1
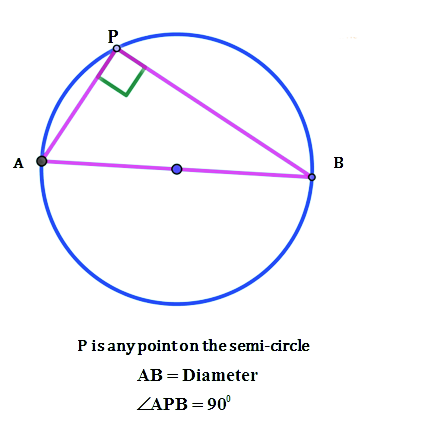
Theorem # 2
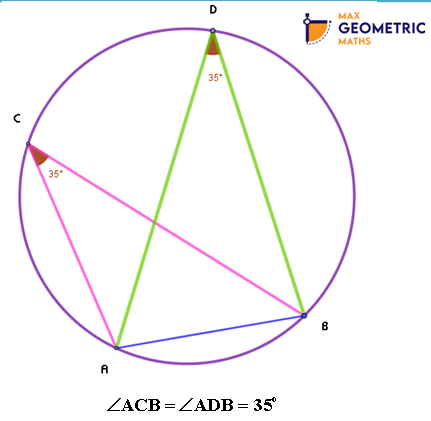
Theorem # 3
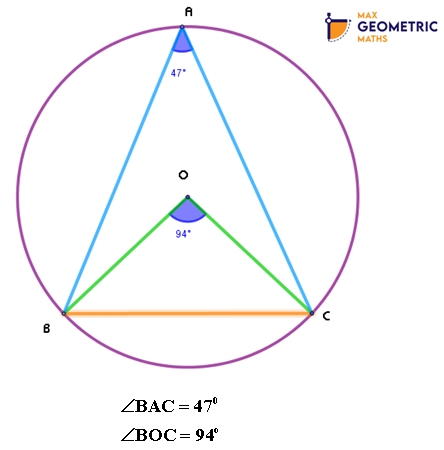
Theorem # 4
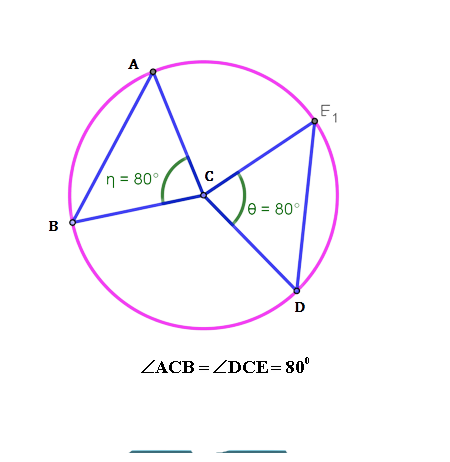
Chords in Circles
Theorem # 1
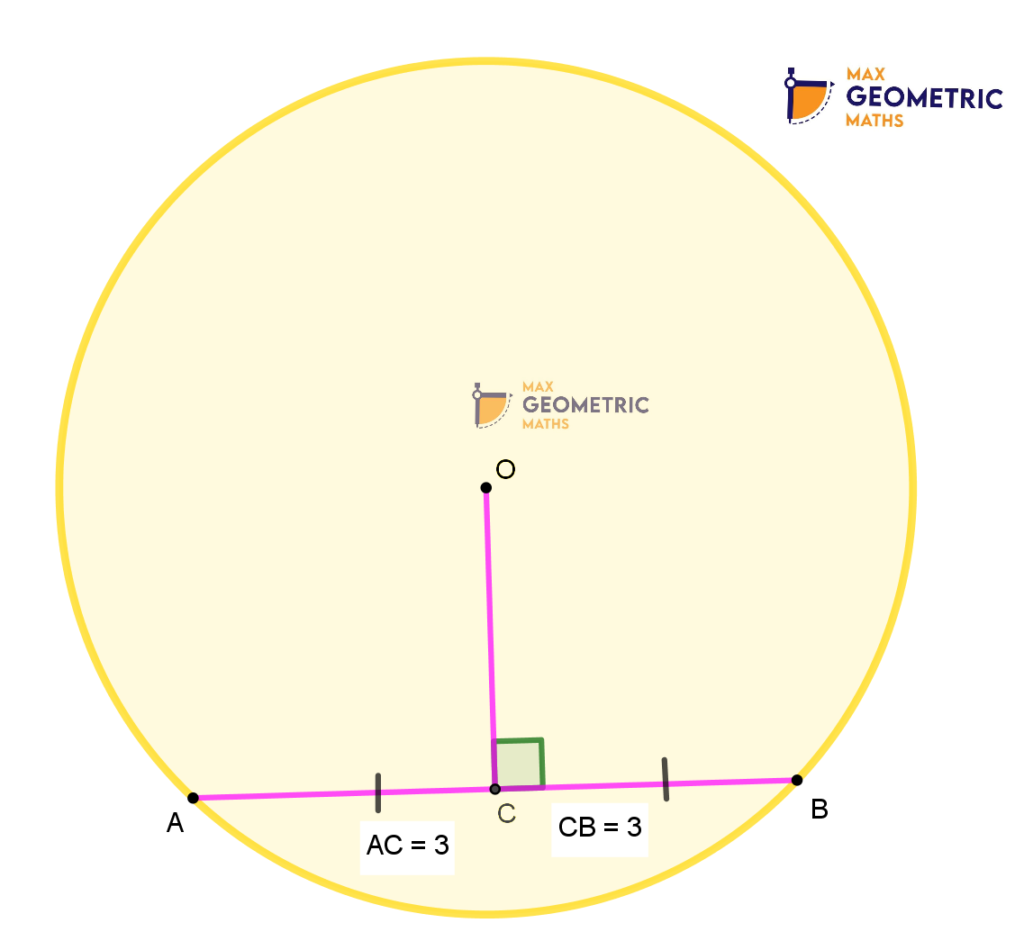
1. The Perpendicular drawn from the centre to a chord bisects the chord.
Conversly, A line drawn from the centre to bisect a chord is always perpendicular to the chord.
2. Perpendicular bisector of every chord of a circle always passes through the centre.
Here, OC, Perpendicular drawn from the centre ‘O’ bisects the chord AB.
AC = CB = 3
Theorem # 2
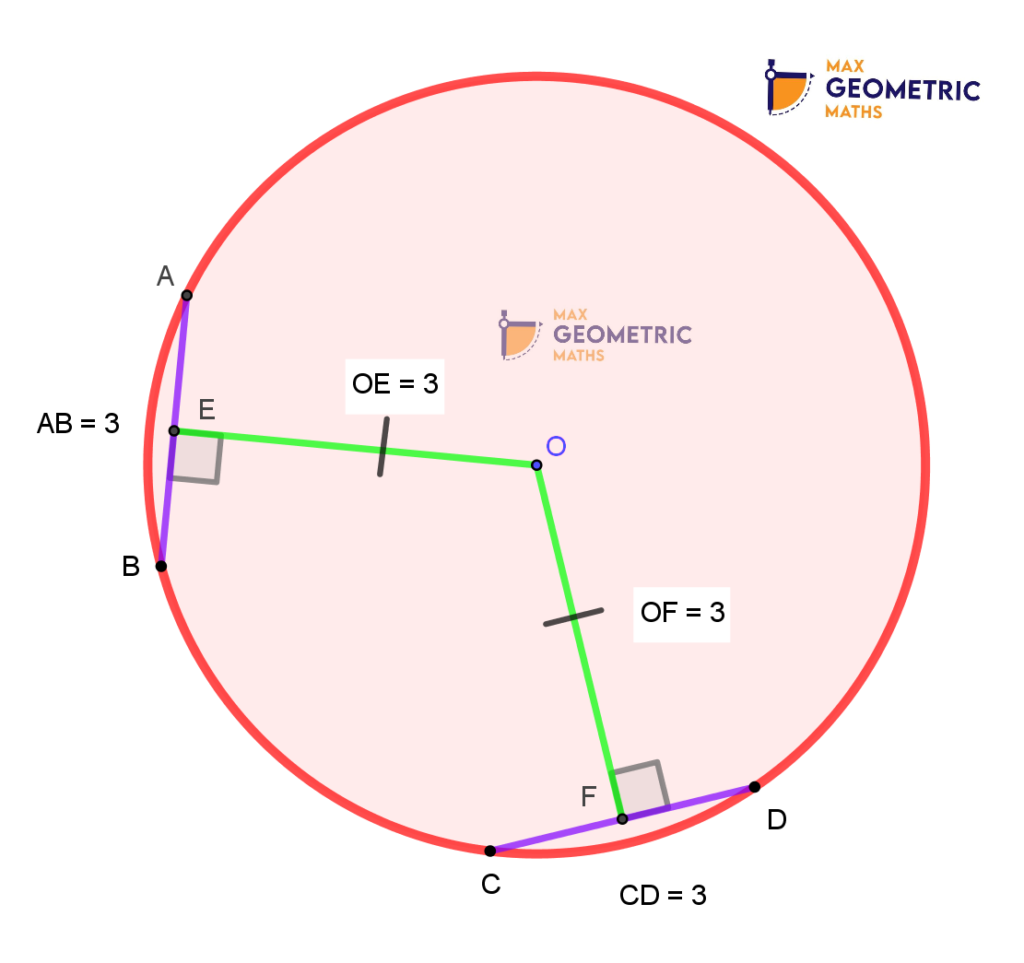
Equal chords are equidistant from the centre.
Conversly, Chords of a circle, equidistant from the centre of the circle are equal.
AB & CD are the equal chords.
They are equidistant from the centre.
(OE = OF = 3)
Theorem # 3
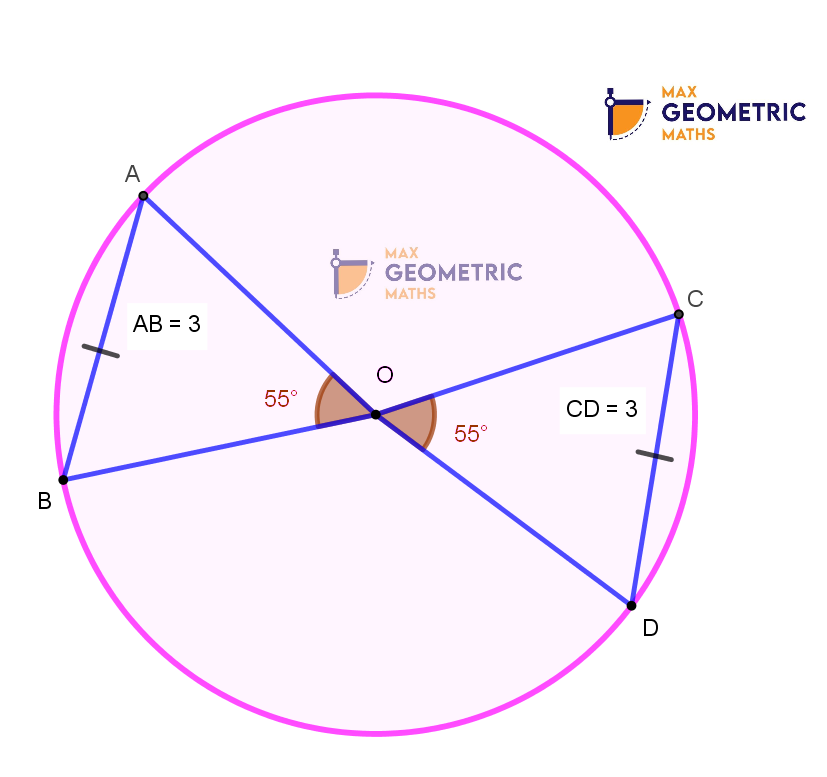
Two equal chords of a circle subtend equal angles at the centre.
AB & CD are equal chords subtending equal angles at the centre.
They are equidistant from the centre.
∠AOB = ∠COD = 55
Theorem # 4
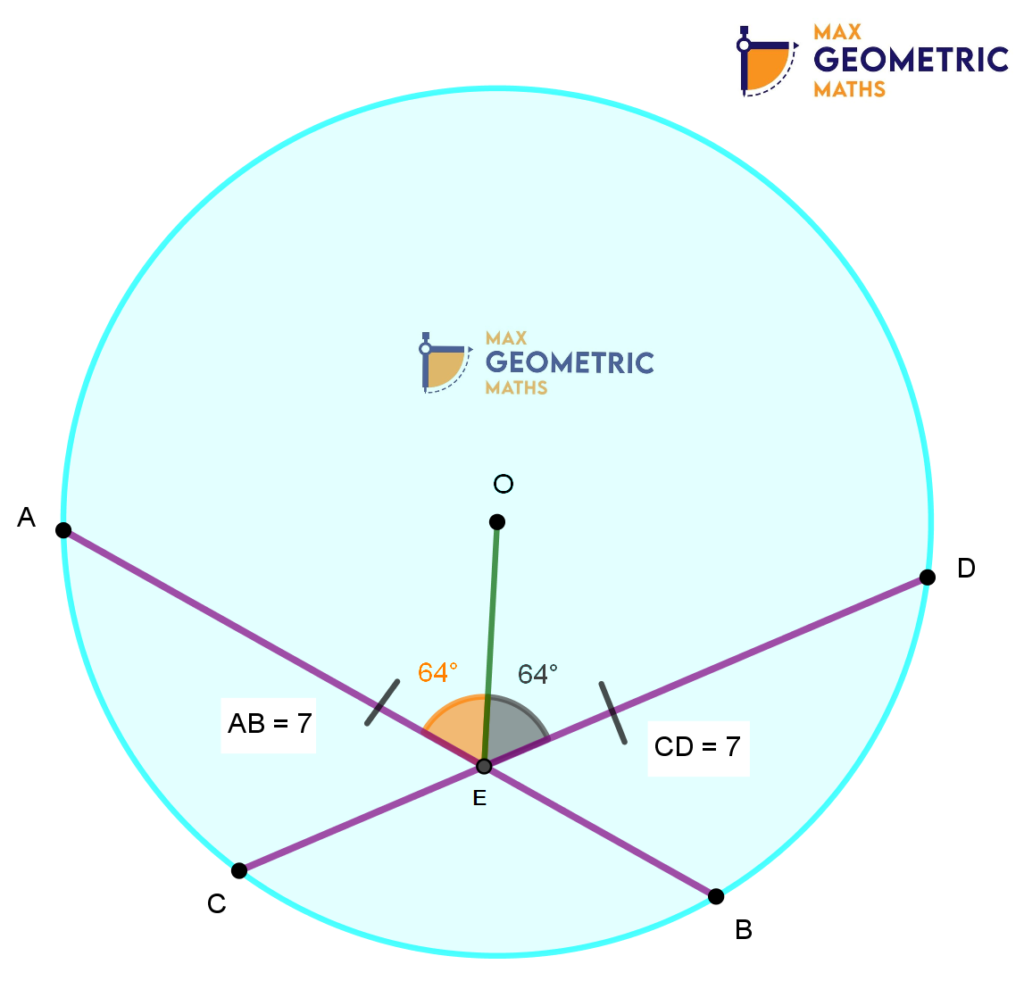
Chords AB & CD of a circle with centre ‘O’ intersect at E. If OE bisects ∠AED, then the chords AB & CD are equal.
Theorem # 5
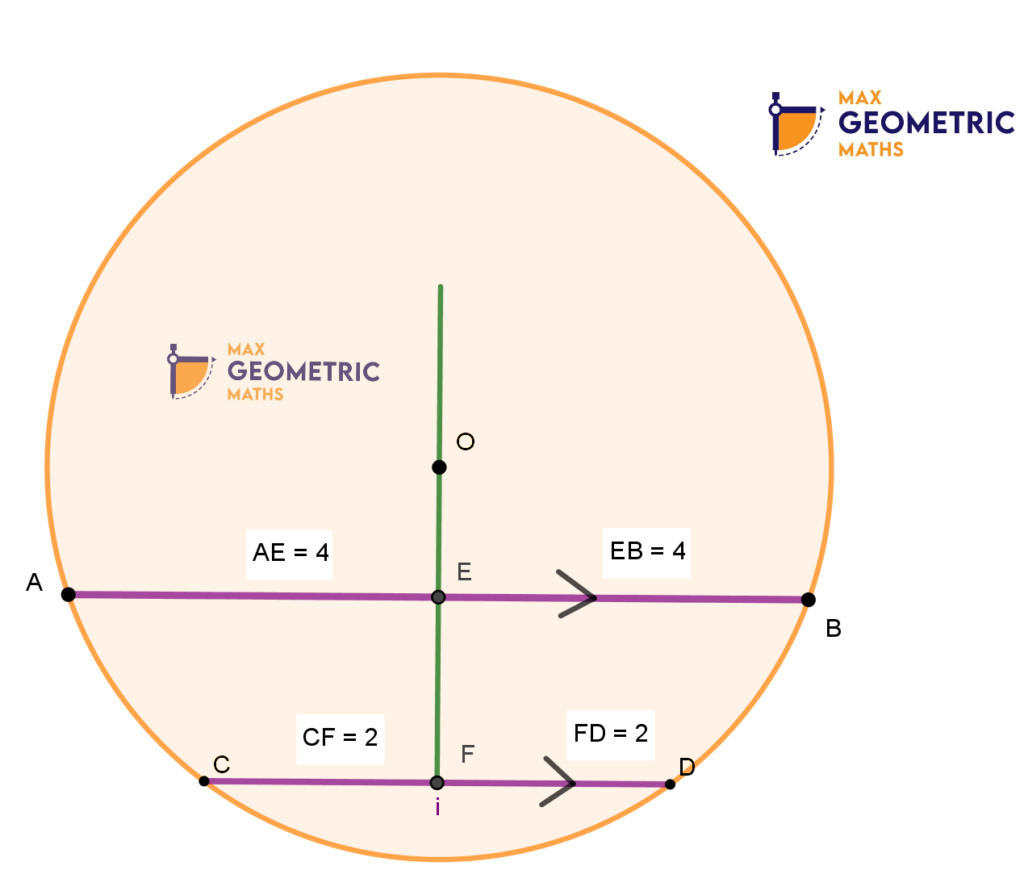
The line segment joining the mid-points of two parallel chords of a circle always passes through the centre.
AB & CD are Parallel chords.
E & F are midpoints of AB & CD.
The line FE passes through the centre ‘O’
Theorem # 6
Chords cut each other internally
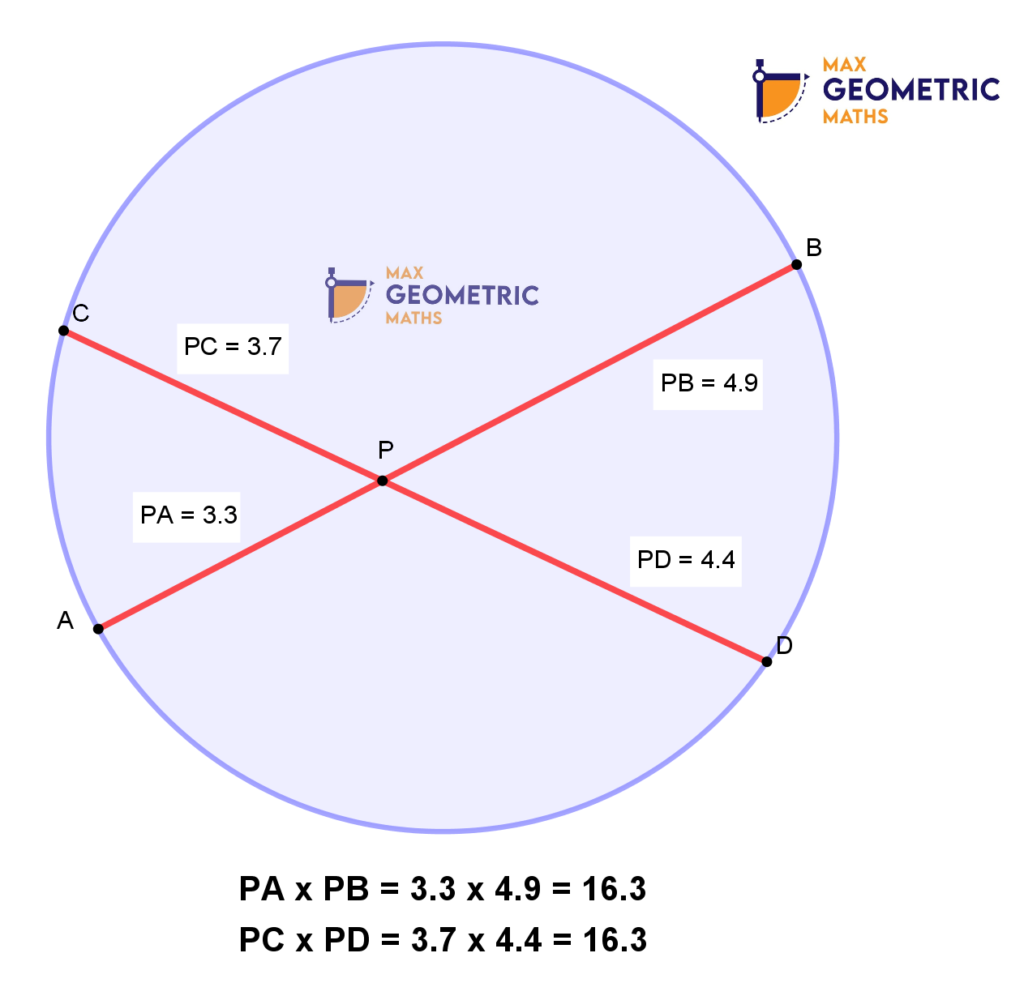
Chords cut each other externally
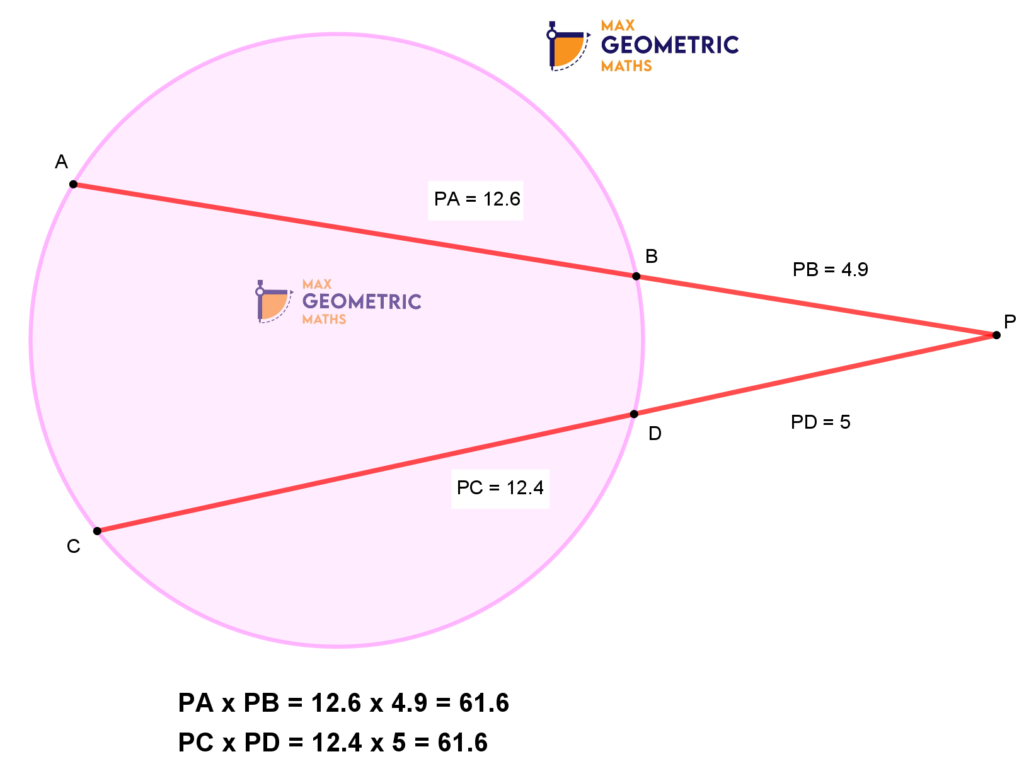
AB & CD are two chords of a circle intersecting at ‘P’ internally or externally, then PA x PB=PC x PD. And, if the chords are equal then PA=PC & PB=PD.
Theorem # 7
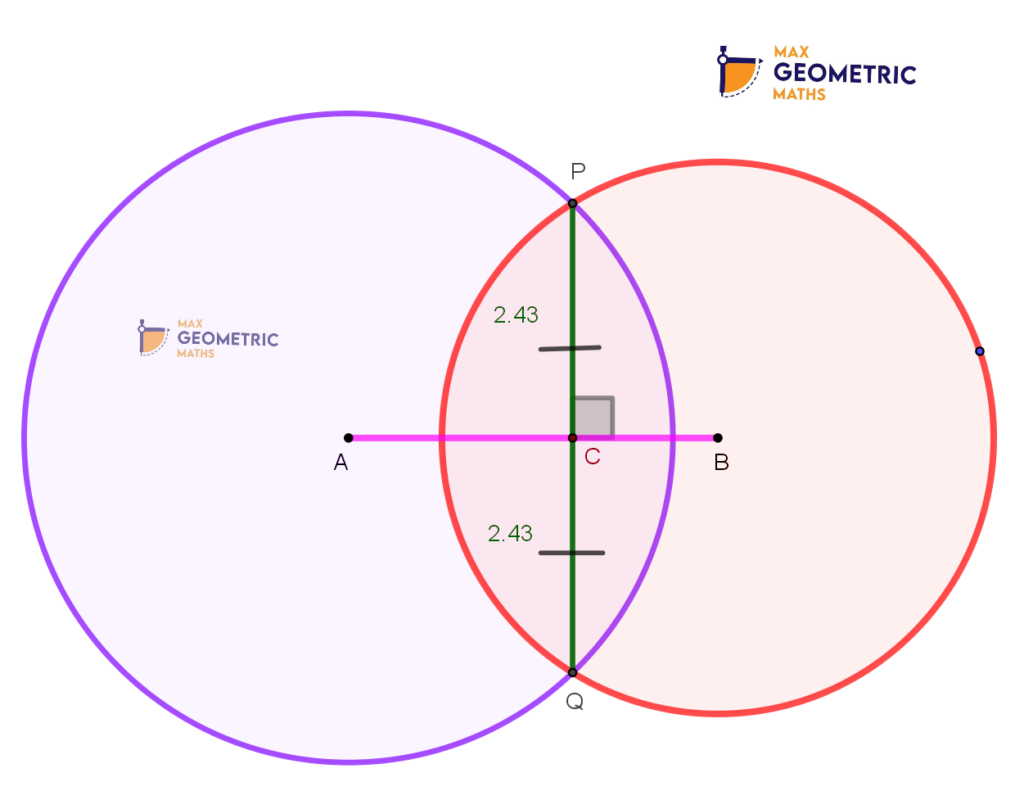
Two Circles with centres A & B intersect each other at points P & Q. Then the line joining the centres bisect the common chord PQ perpendicularly.
Theorem # 8
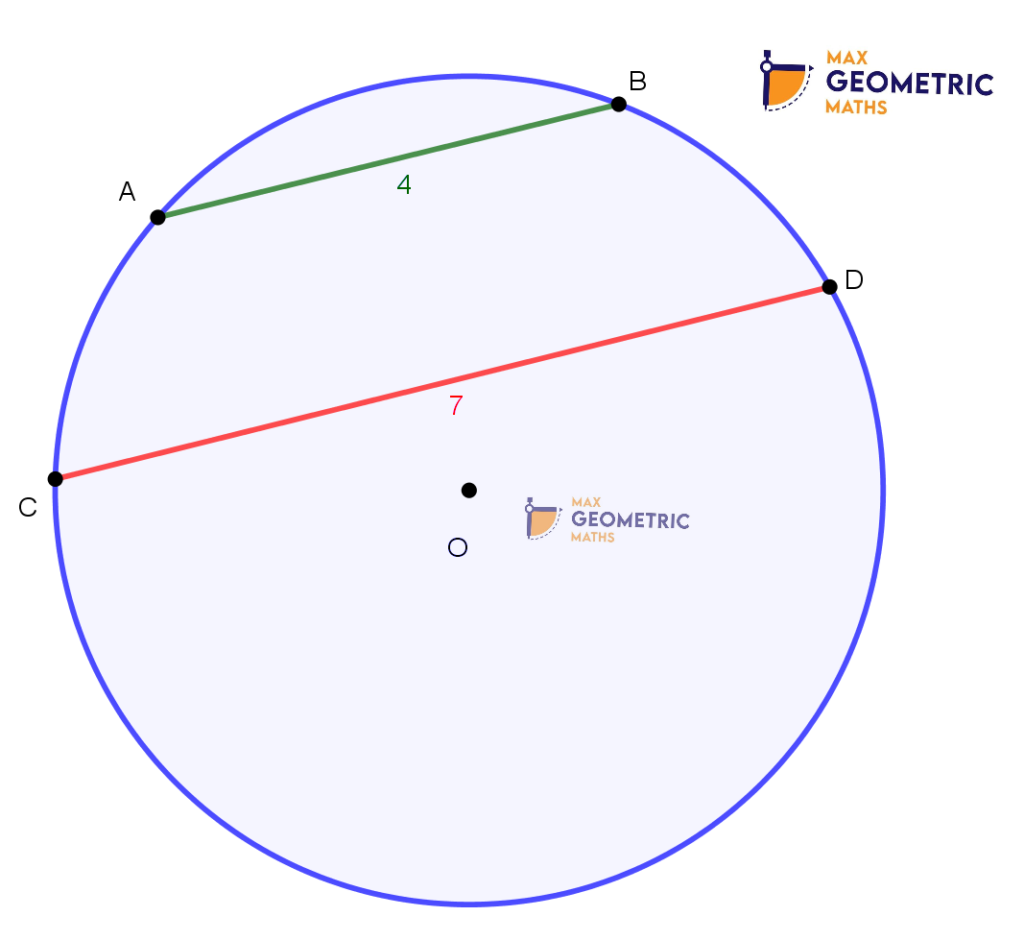
Out of two unequal chords of a circle, the longer chord will be closer to the centre than the shorter chord.
AB = 4 is far away from the centre.
CD = 7 is closer to centre.
Theorem # 9
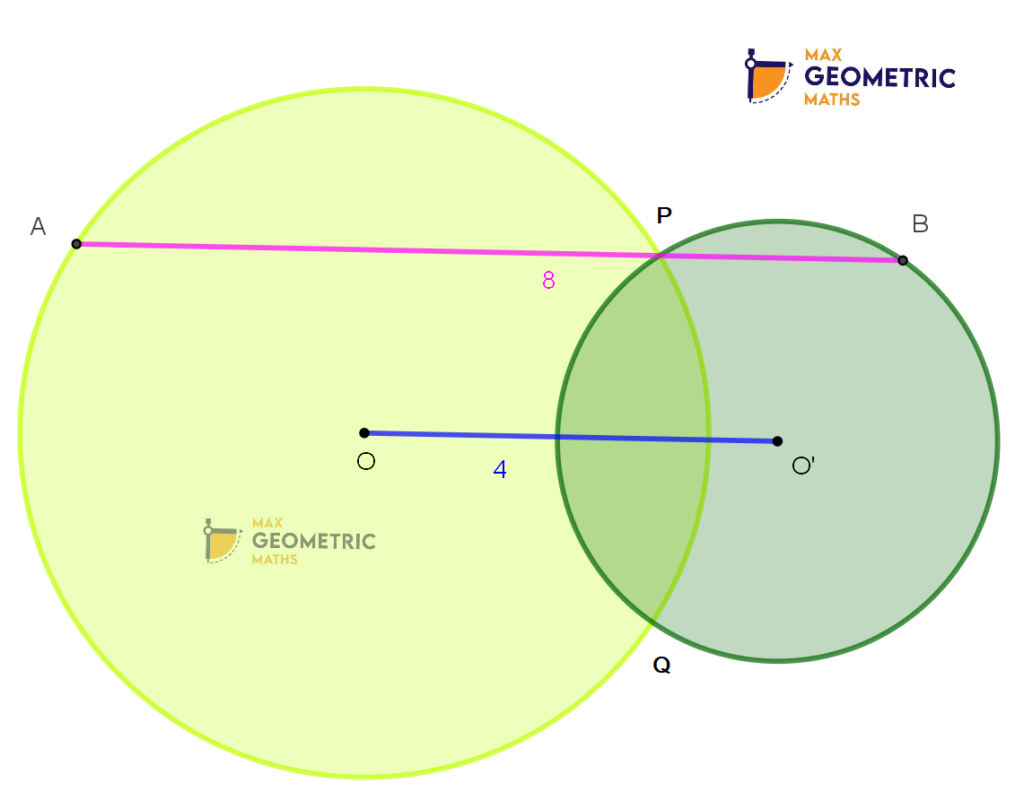
Two circles with centres O & ‘O’ intersect each other at points P & Q. The straight line APB is parallel to the line joining centres OO’ & OO’ = (1/2) AB
Theorem # 10
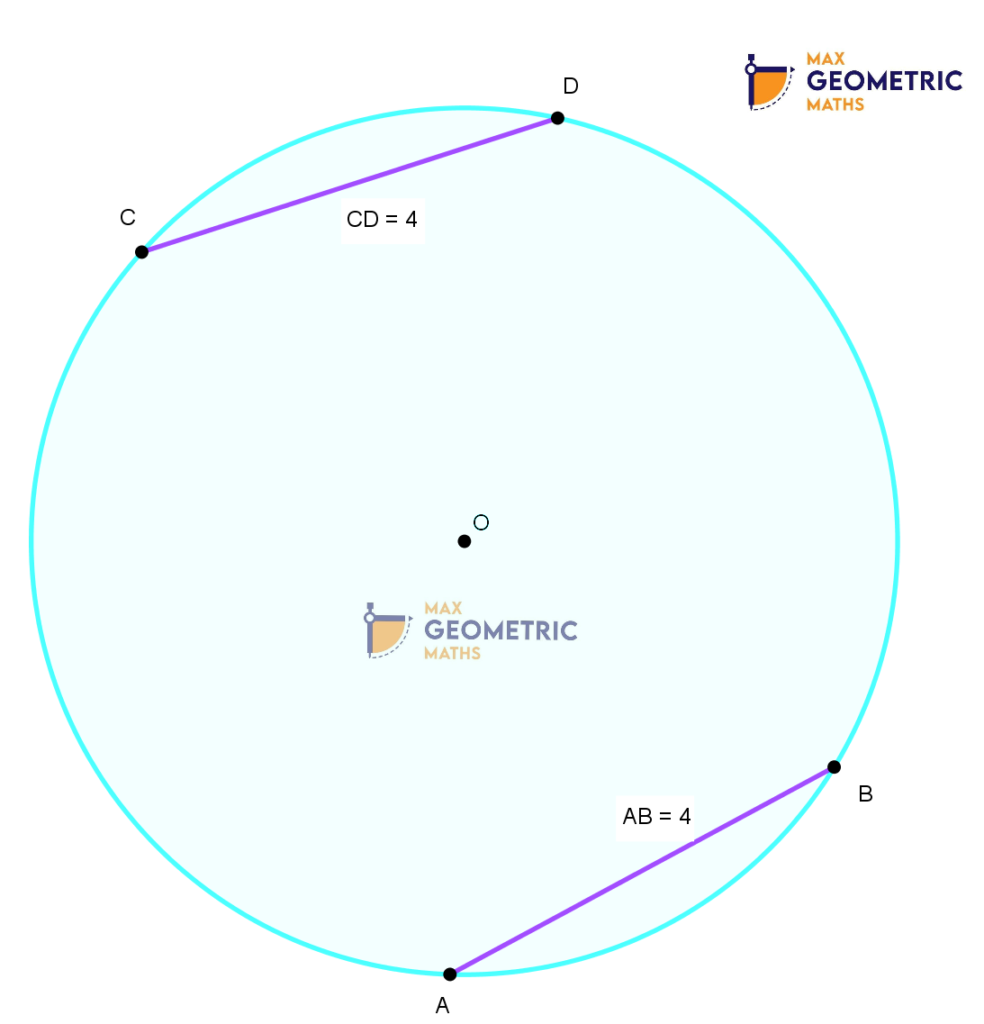
1. If chords of a circle are equal in length, then the corresponding arcs will be congruent.
Similarly, if arcs are congruent, then the corresponding chords will be equal.
2. The segments of one chord are equal to corresponding segments of the other chord if two equal chords of a circle intersect within the circle.
Theorem # 11
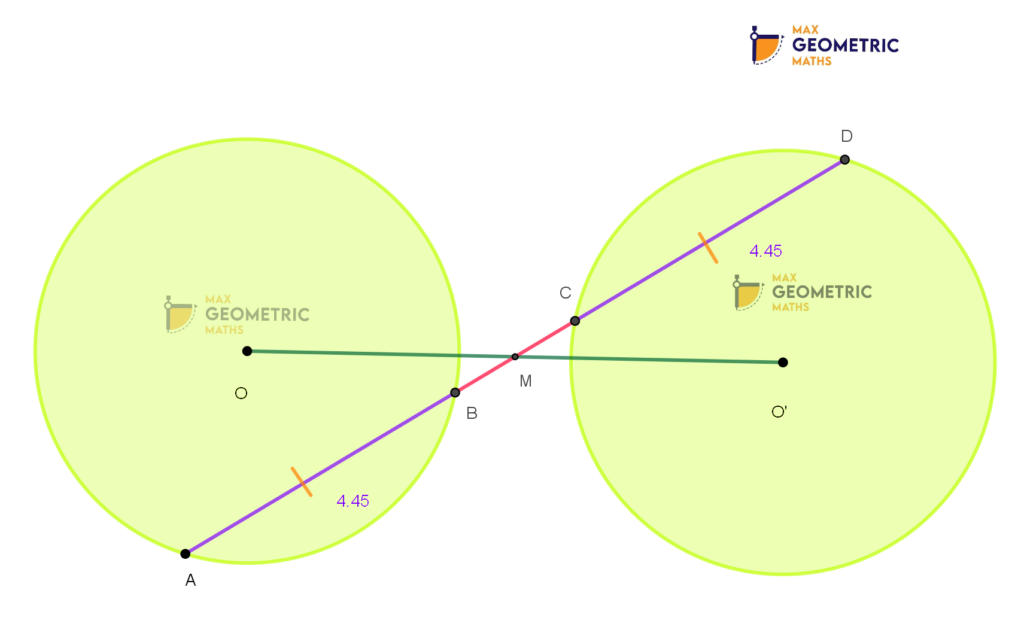
A straight line is drawn cutting two equal circles & passing through the mid-point M of the line joining the centres O & O’. Then the chords AB & CD which are intercepted by the two circles are equal.
Here, AB = CD = 4.45
Theorem # 12
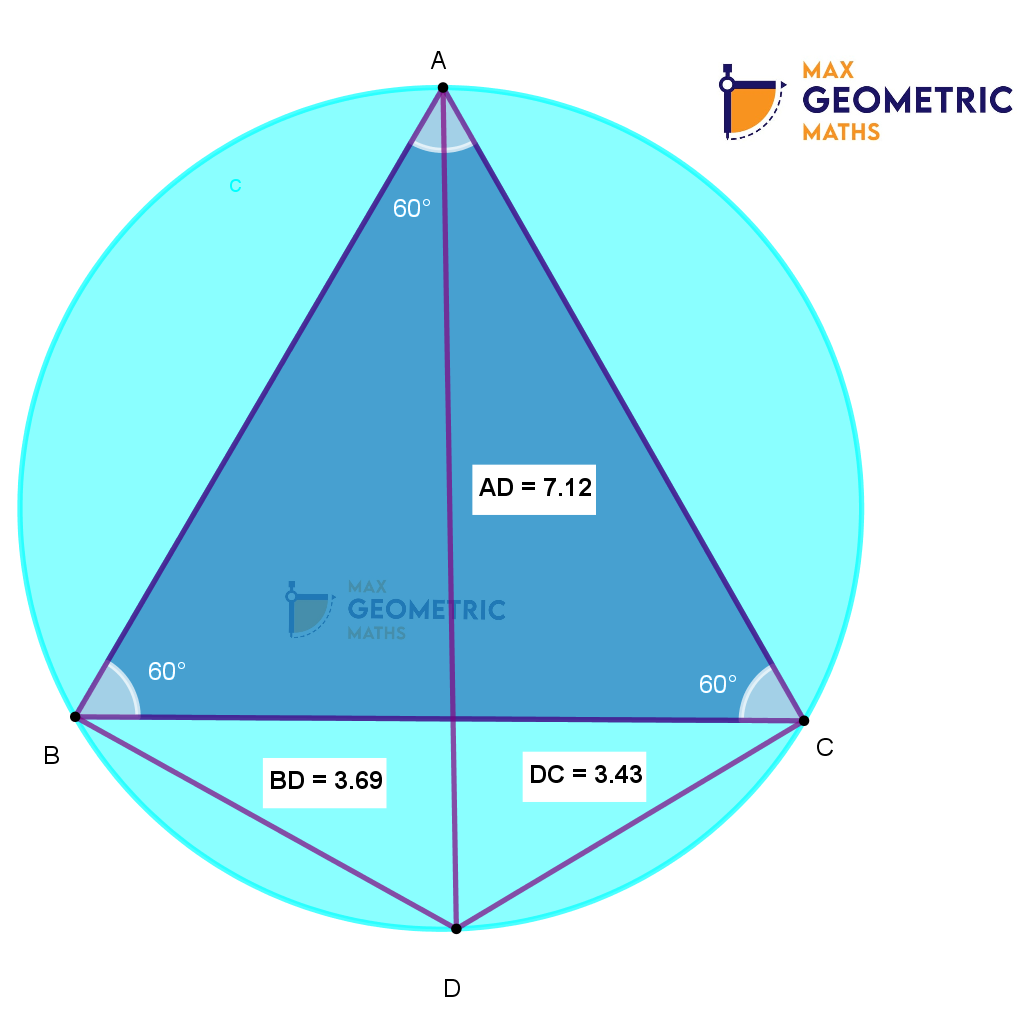
ABC is an equilateral triangle inscribed in a circle. ‘D’ is a point on minor arc BC. Prove AD = BD + DC
Tangents in Circles
Theorem 1
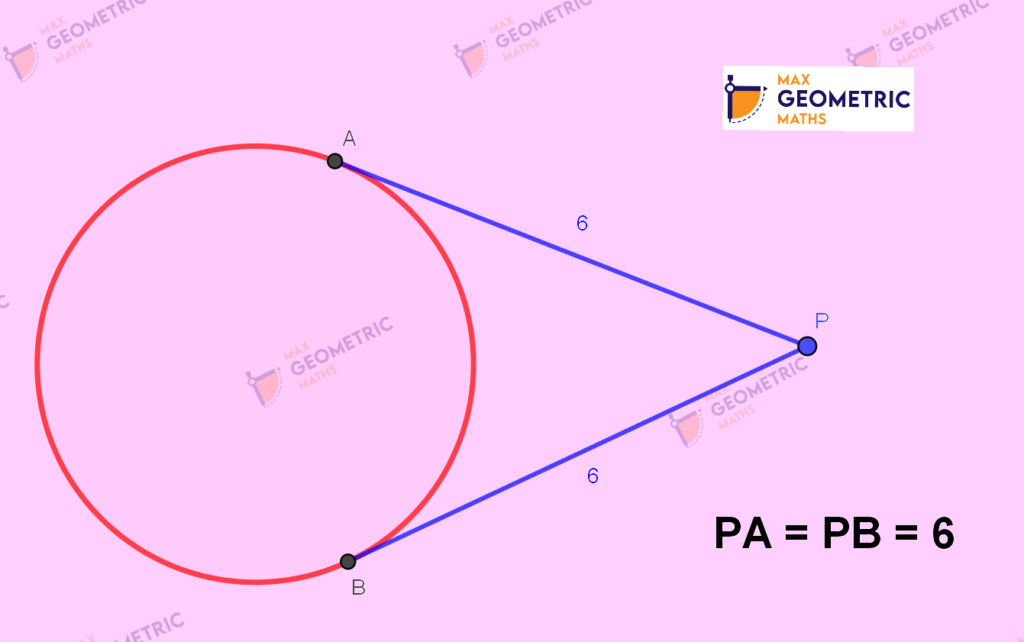
Only two tangents can be drawn from an external point to a circle.
The length of the two tangents drawn from a common exterior to the circle are equal.
Theorem 2
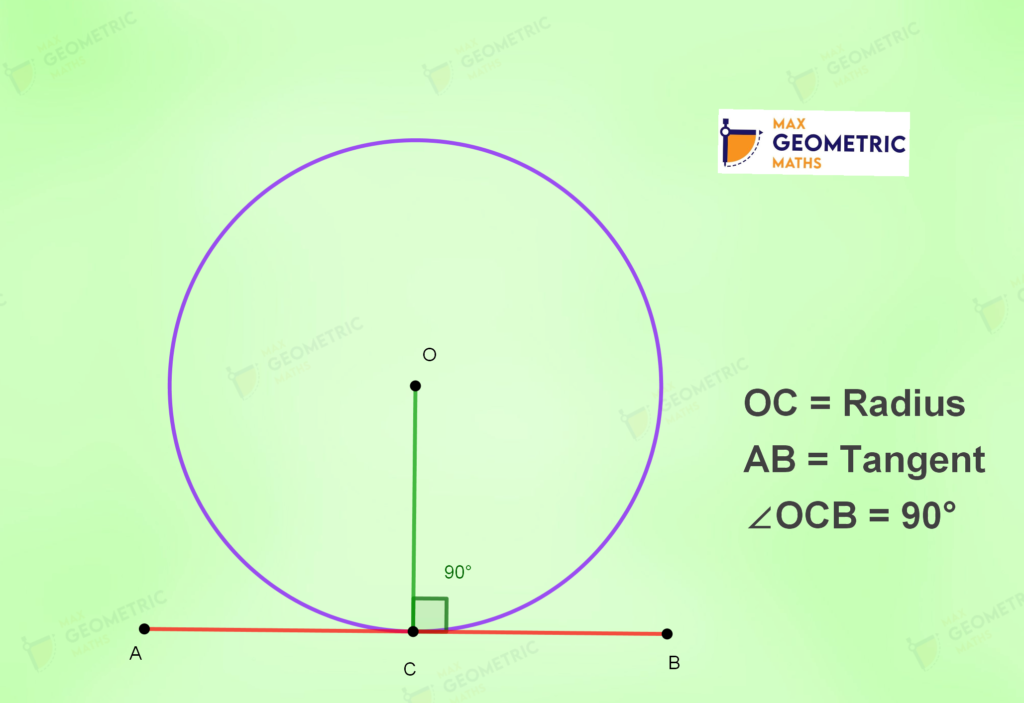
Relation between Radius & Tangent:
The angle between the radius & tangent is 90 0 at the point of contact.
The line perpendicular to a tangent at the point of tangency will always pass through the centre.
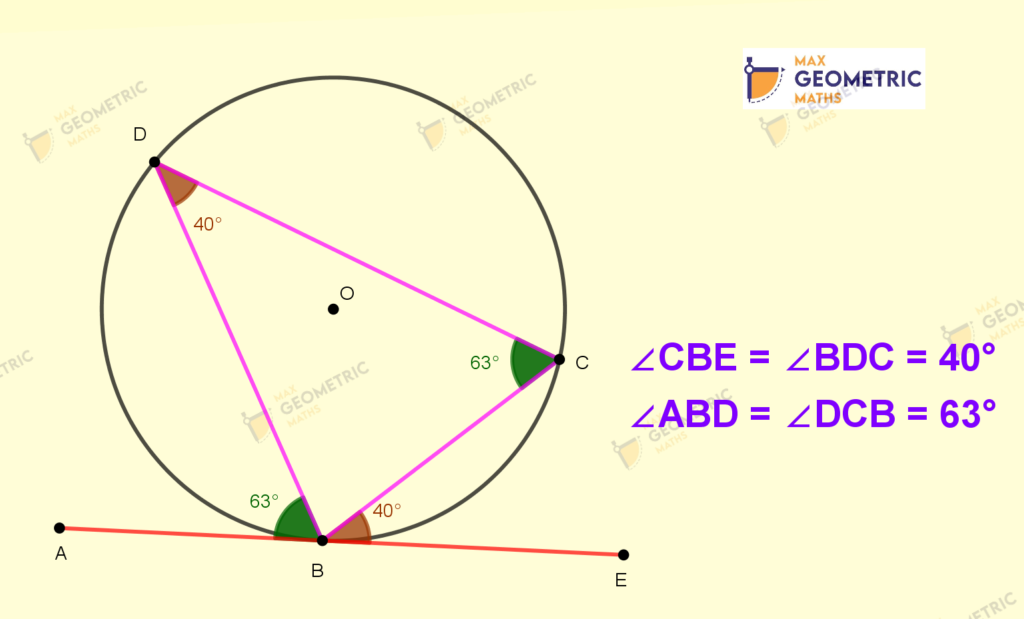
Alternate Segment Theorem (Or) Tangent Chord Theorem
The angle that lies between a chord and a tangent through any one of the end points of the chord is equal to the angle in the alternate segment.
And, Conversly ‘If a line is drawn through an end point of a chord of a circle so that the angle formed with the chord is equal to the angle subtended by the chord in the alternate segment, then the line is a tangent to the circle.
Author’s Creation in Circles
1. Question:
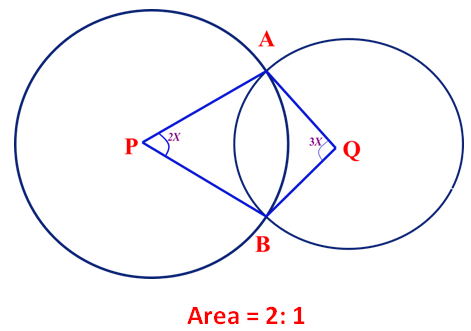
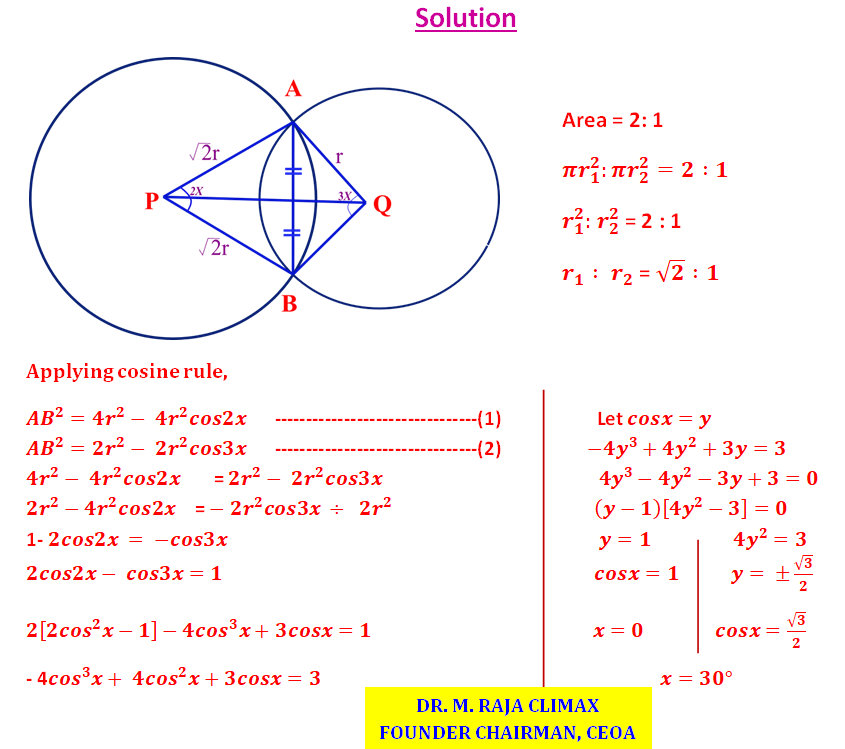
Two circles with centres at P and Q are having areas in the ratio of 2:1. They intersect each other at A & B. If ∠APB = 2x and ∠AQB = 3x, find the value of x.
Question created by
Dr.M.Raja Climax
Founder Chairman, CEOA
2. Question:
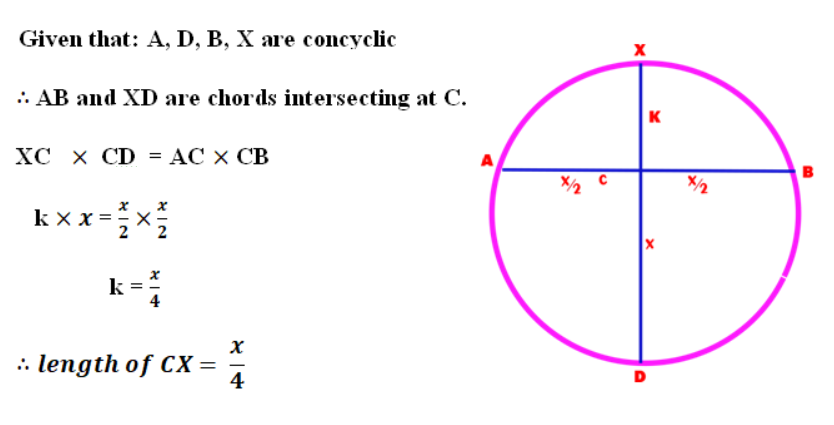
Good Friday Problem
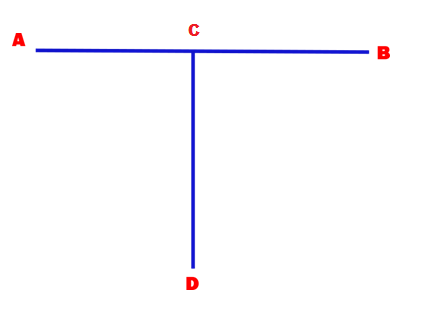
Raja, a Christian Mathematician, wanted to make a cross for Good Friday. First, he took two wooden pieces AB and CD and made a “T shape” as shown in the picture.
AB = CD = x ft.
C is also the midpoint of AB. Now he has to affix a small piece CX upon C so as to make the cross complete. He wanted to make this in such a way that X lies on the circumcircle of triangle ADB.
Find the length of CX in terms of ‘x’.
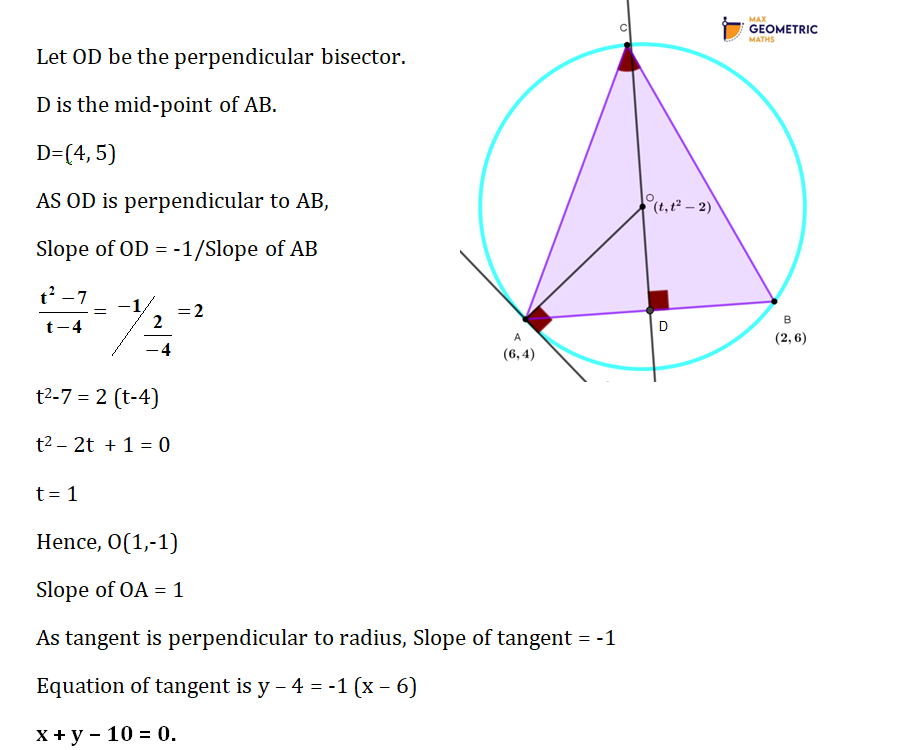
3. Question:
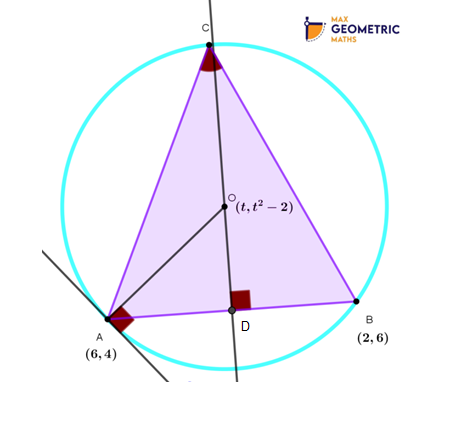
A(6,4) and B(2,6) are vertices of a Δ ABC and C is unknown. The circumcentre of the said Δ ABC is O(t, t²-2). Find the equation of the tangent to the circle at A.
4. Question:
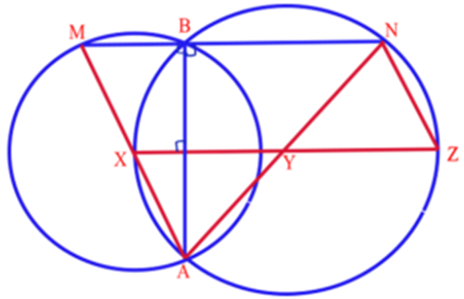
The story behind the following question: Our author’s friend Mr. Lakshmana Moorthy has sent a challenging problem on two circles for solving. Our author solved the problem in no time & while sending the solution to his friend, it has become habitual for our author to send one or two & sometimes even more additional results as compliments along with the solution for receiving such challenging questions. The following is one such question.
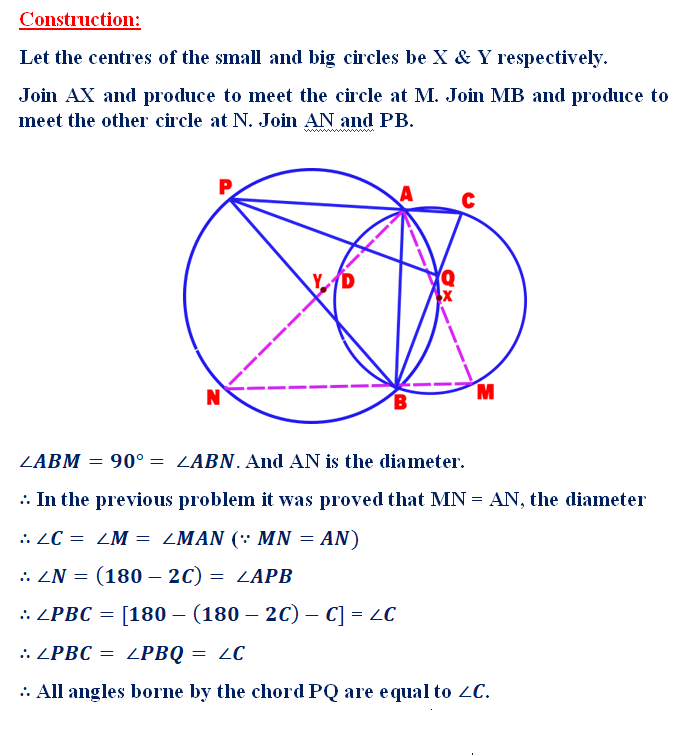
Two circles with unequal radius intersect each other at A & B and the circumference of the bigger circle passes through the centre of the smaller circle. Through B, a line perpendicular to AB is drawn cutting the circles at M & N. Prove that MN equals the diameter of the bigger circle.
5. Question:
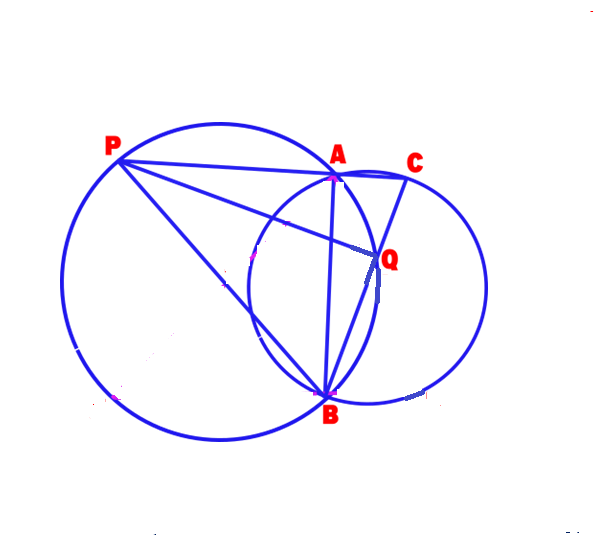
The story behind the following question: Our author’s friend Mr. Lakshmana Moorthy found that the angle subtended by PQ = ∠C while drawing the figure in GeoGebra Software but he was not able to prove it theoritically. So he sent the problem to our author for solving it. Here is the solution given by our author.
Two circles with unequal radius intersect each other at A & B and the circumference of the bigger circle passes through the centre of the smaller circle. C is a point on major arc AB of smaller circle such that CA produced cuts a bigger circle at P & CB cuts the minor arc AB of the bigger circle at Q. Prove that the angle borne by PQ on its major arc = ∠C .
6. Question:
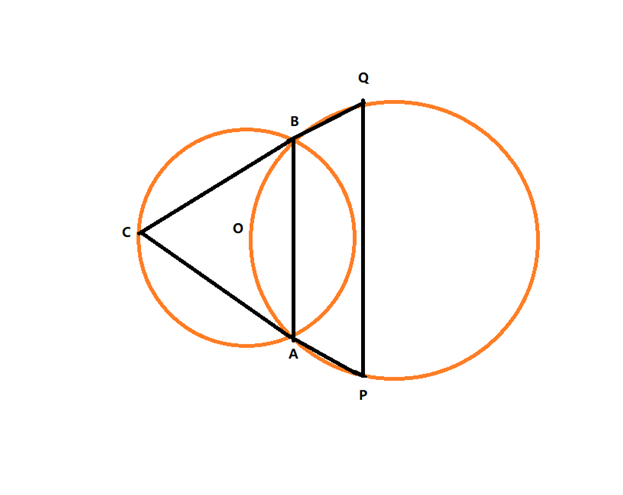
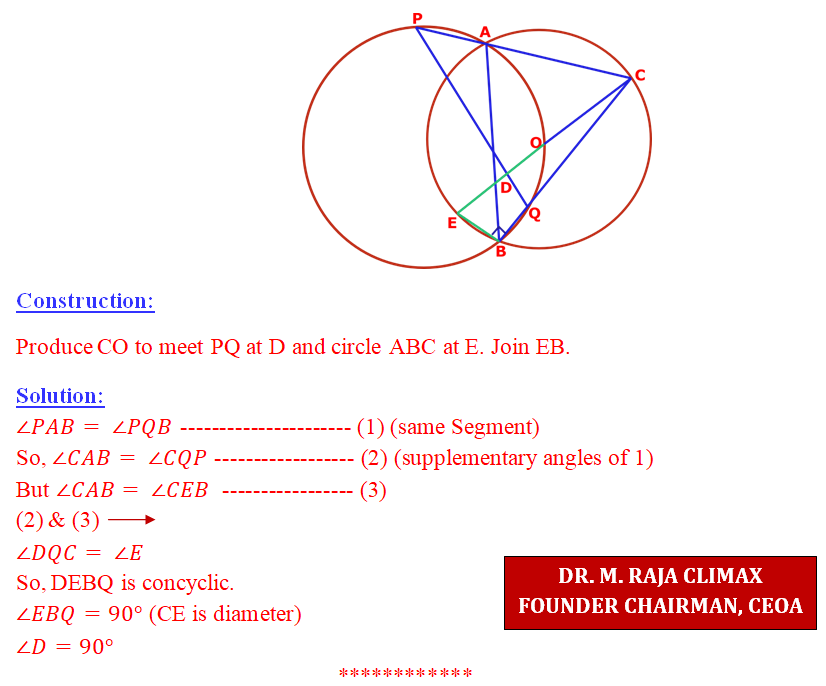
ABC is a triangle inscribed in a circle with circumcentre O. Another circle is drawn so as to go through A, O & B. CA & CB produced cut the second circle at P & Q respectively. Prove that the angle subtended by PQ = ∠C.
7. Question:
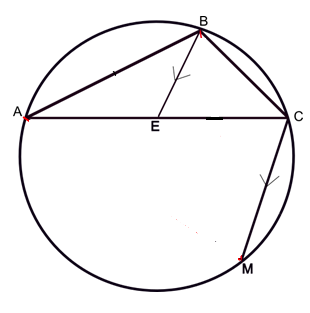
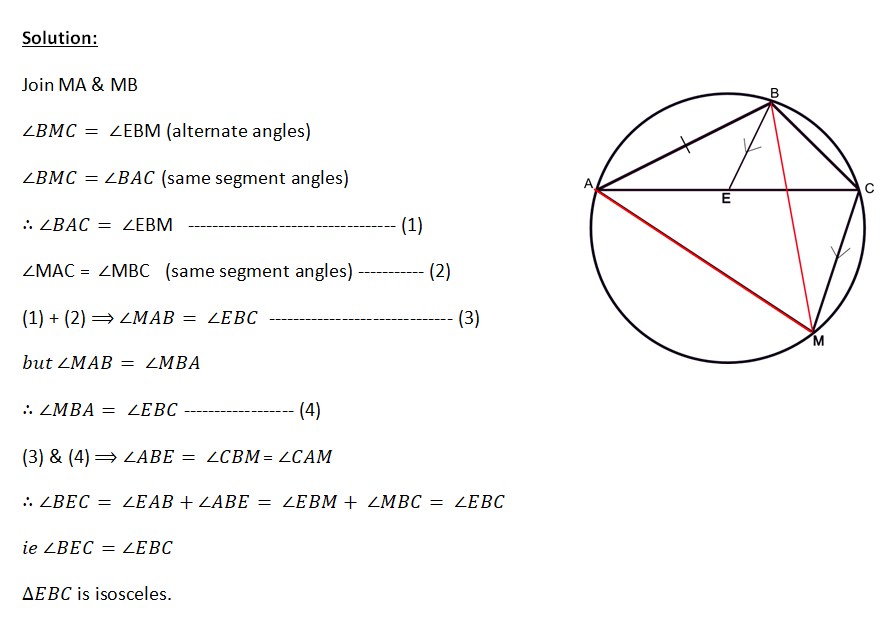
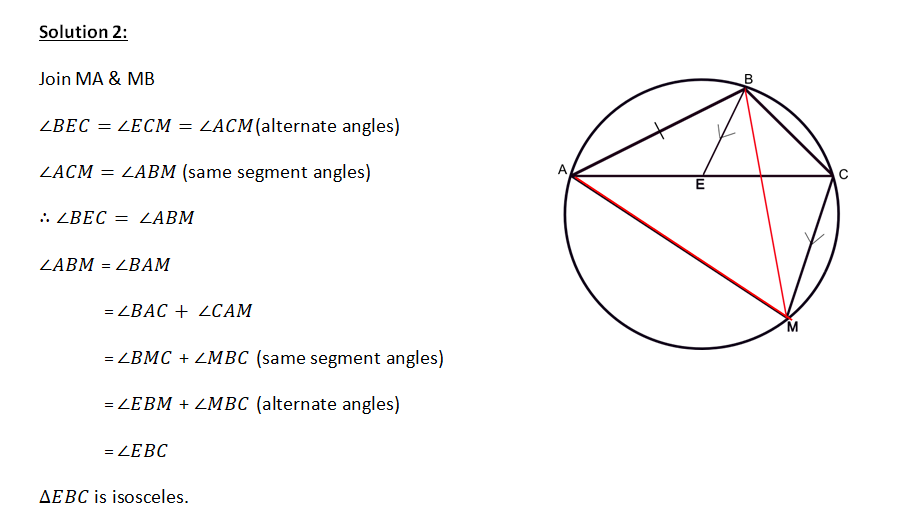
ABC is a triangle inscribed in a circle with AC > BC. M is the midpoint of major arc AB. A line is drawn parallel to MC through B meets AC at E. Prove that is isosceles .
8. Question:
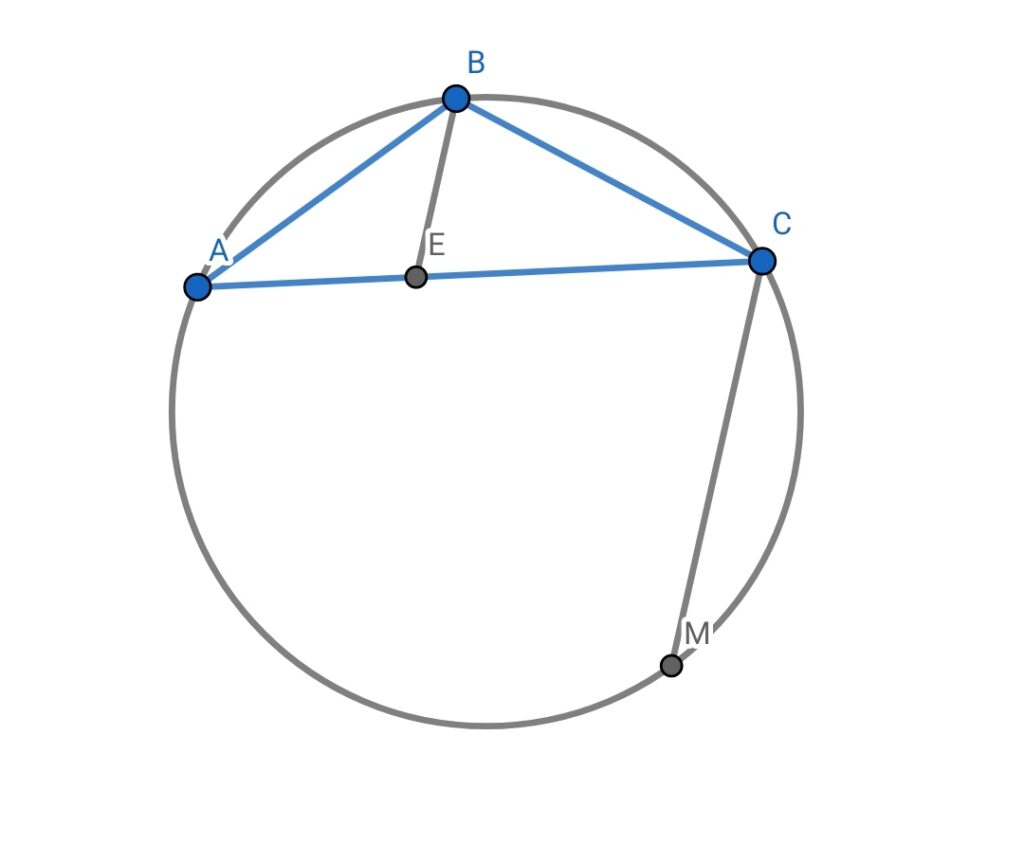
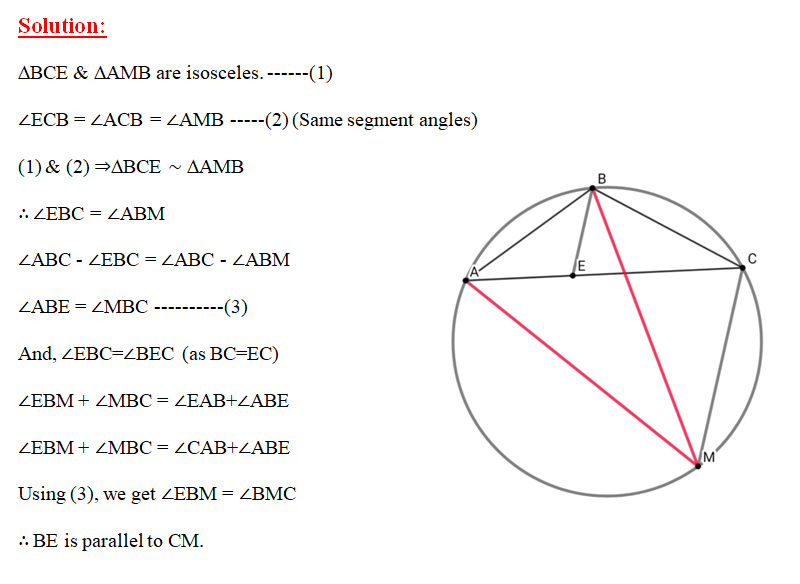
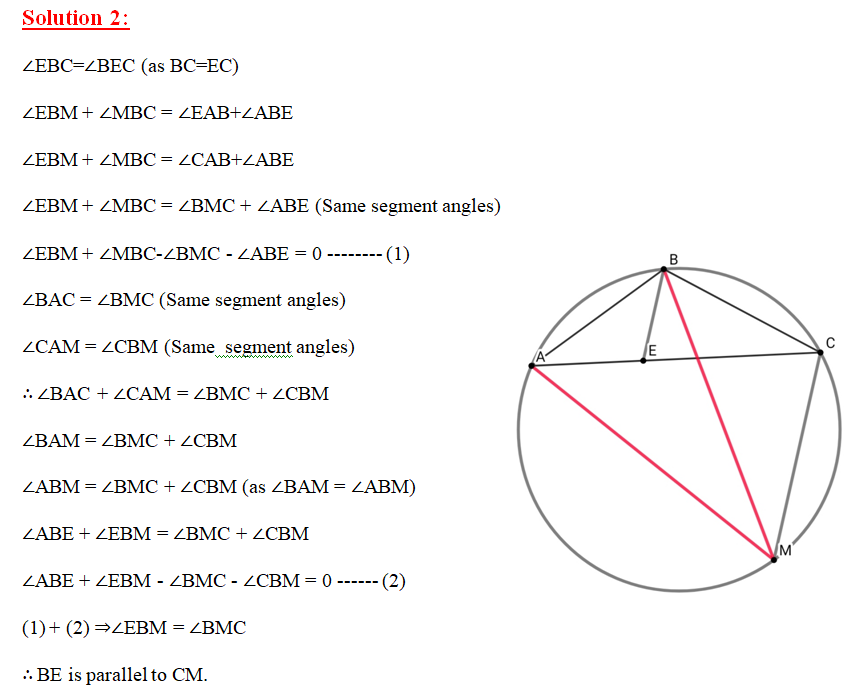
ABC is a triangle inscribed in a circle with AC > BC. M is the midpoint of major arc AB. If E is a point on BC such that BE=EC, then prove that BE is parallel to CM.
9. Question:
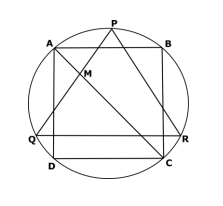
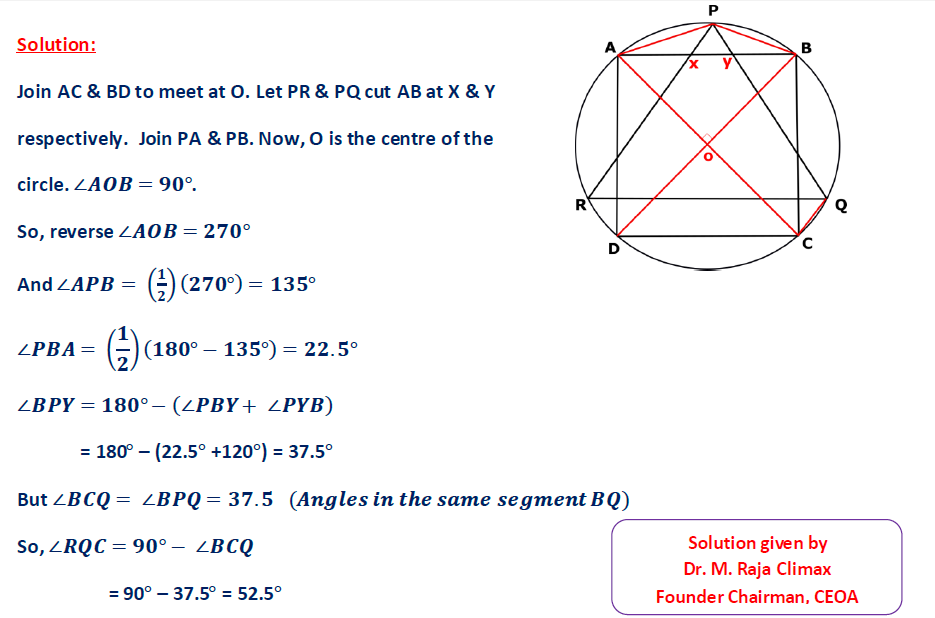
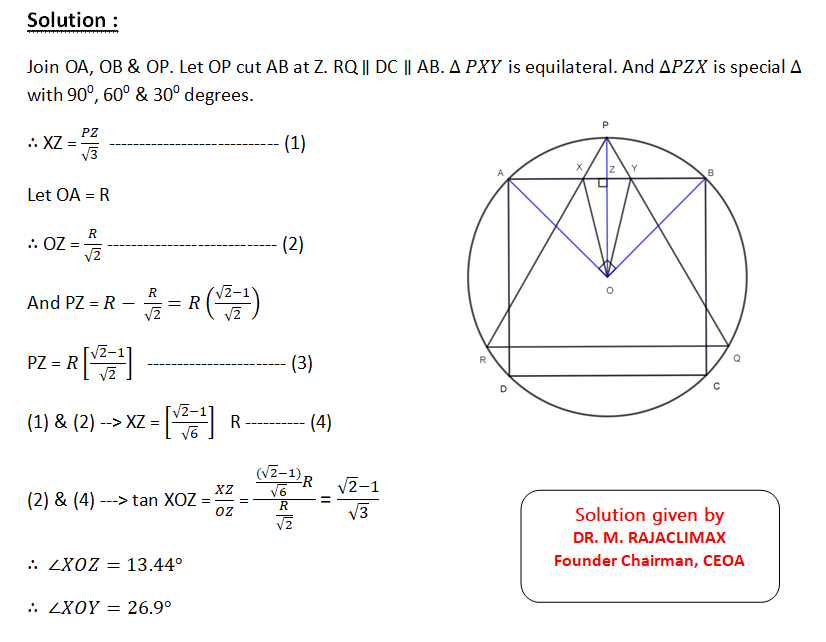
In the given picture, the square ABCD and the equilateral triangle PQR are inscribed in the circle such that QR is parallel to AB & CD. AC & PQ cut at M. Prove that MQ = R, the radius of the circle.
10. Question:
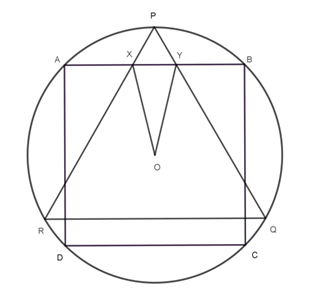
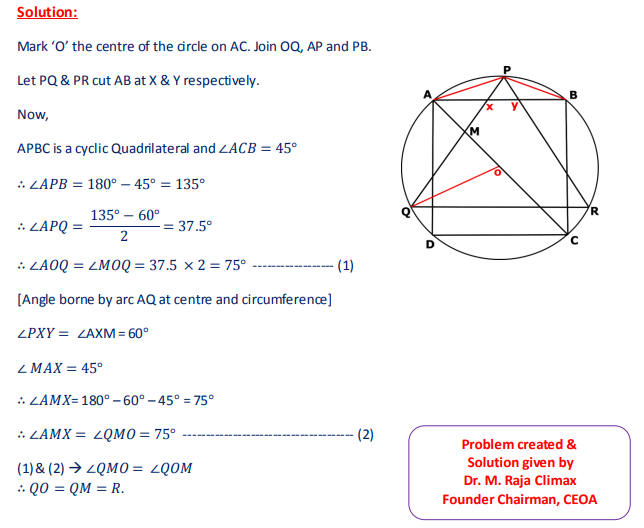
A square ABCD and an equilateral triangle PQR are inscribed in a circle centered at O in such a way that AB is parallel to QR. The sides PQ and PR of the triangle meet the side AB of the square at X and Y respectively. Find the value of ∠RQC
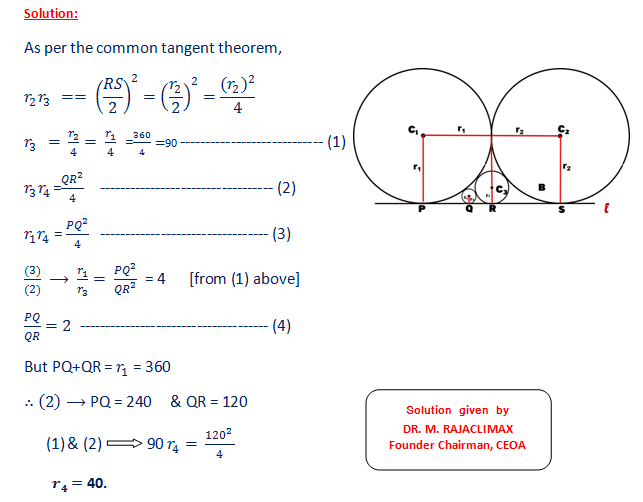
11. Common Tangent Theorem

12. Question:
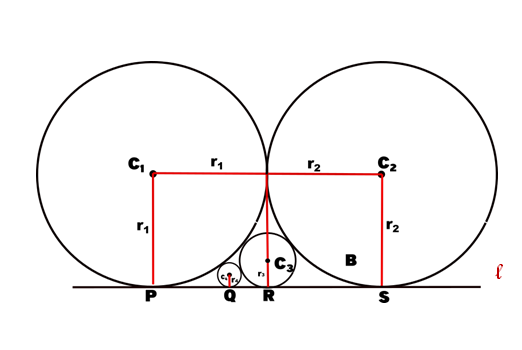
As shown in the figure below, circles C1 of C2 of radius 360 are tangent to each other, and both tangent to straight l . If circle C3 is tangent to C1, C2 and l ,and circle C4 is tangent to C1, C3 and l , find the radius of C4.
13. Question:
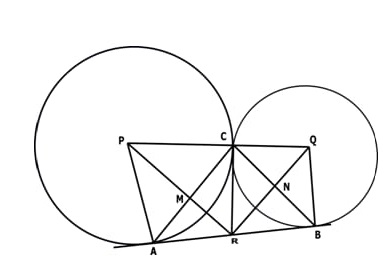
In the picture two circles with centres P & Q touch each other at C. AB is their common tangent. Identify & write down the triangles that are similar to ABC.
Author’s Solution for Challenging Problems in Circles
1. Question:
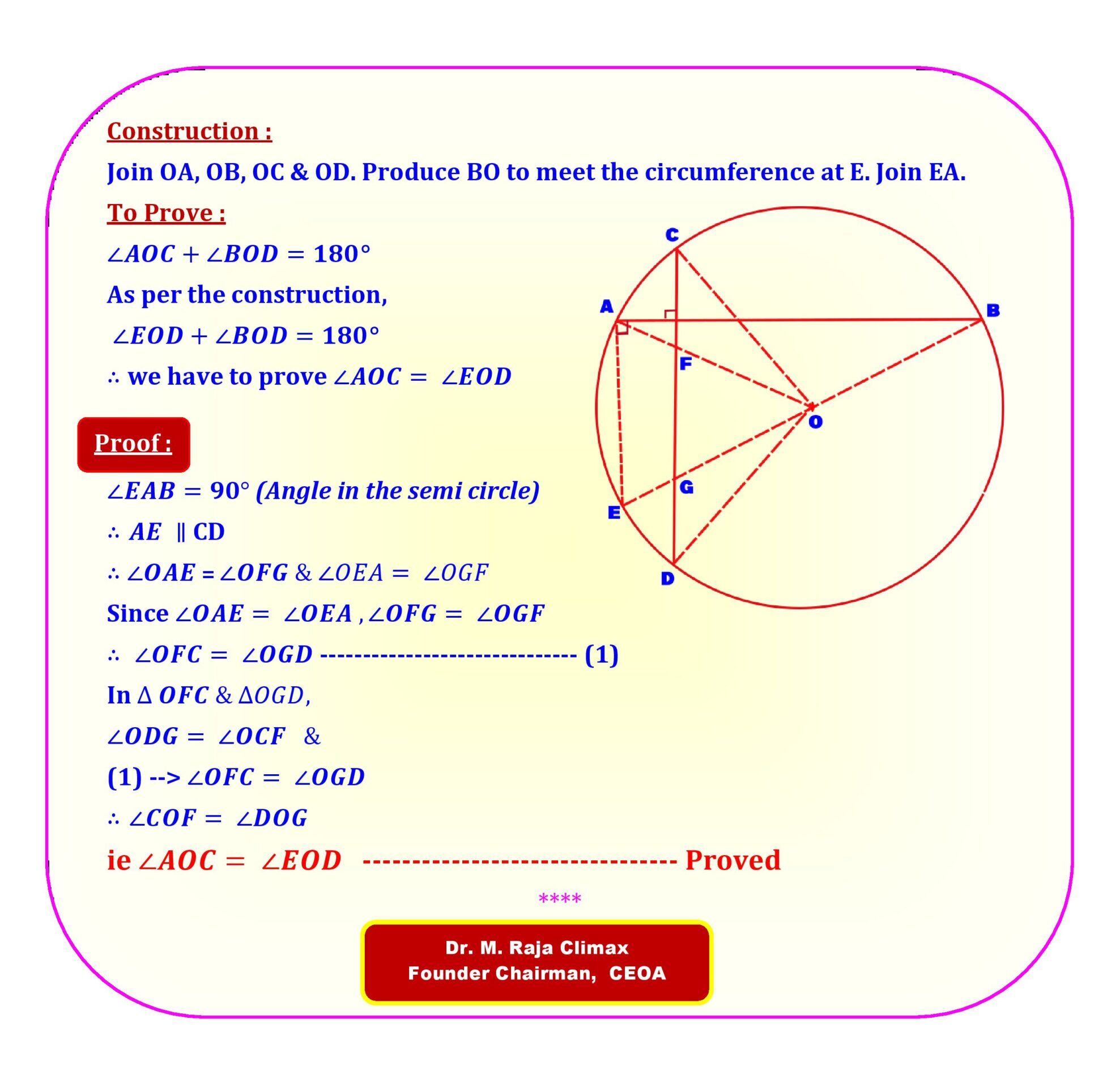
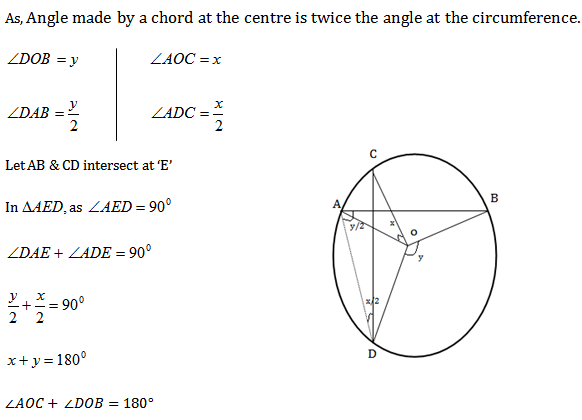
AB & CD are two chords of a circle with centre ‘O’ intersecting each other at right angles. Prove that ∠AOC + ∠BOD = 180
[ Here, is an interesting story behind the problem. This problem was given to our author as an assignment when he was at his SSLC. The teacher has given instruction to do this problem using the theorem ‘The angle made by a chord at the centre is twice the angle at the circumference’ but instead our author has solved this problem in the other way which is beyond his level. Though the teacher initially got angry on looking at the solution (as our author didn’t apply the theorem taught to him), at last he appreciated our author for solving the problem the other way though it is complicated.]
The Teacher’s expected solution is also given below.
3. Question:
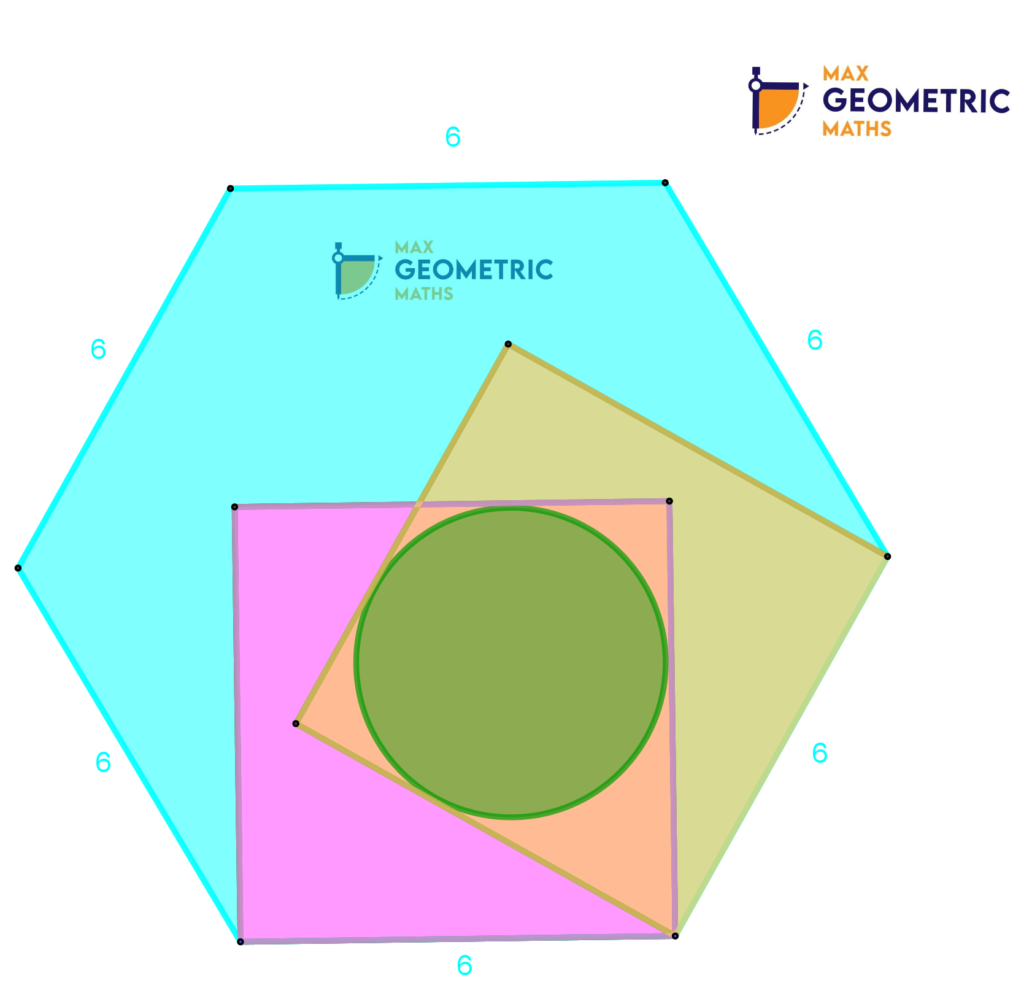
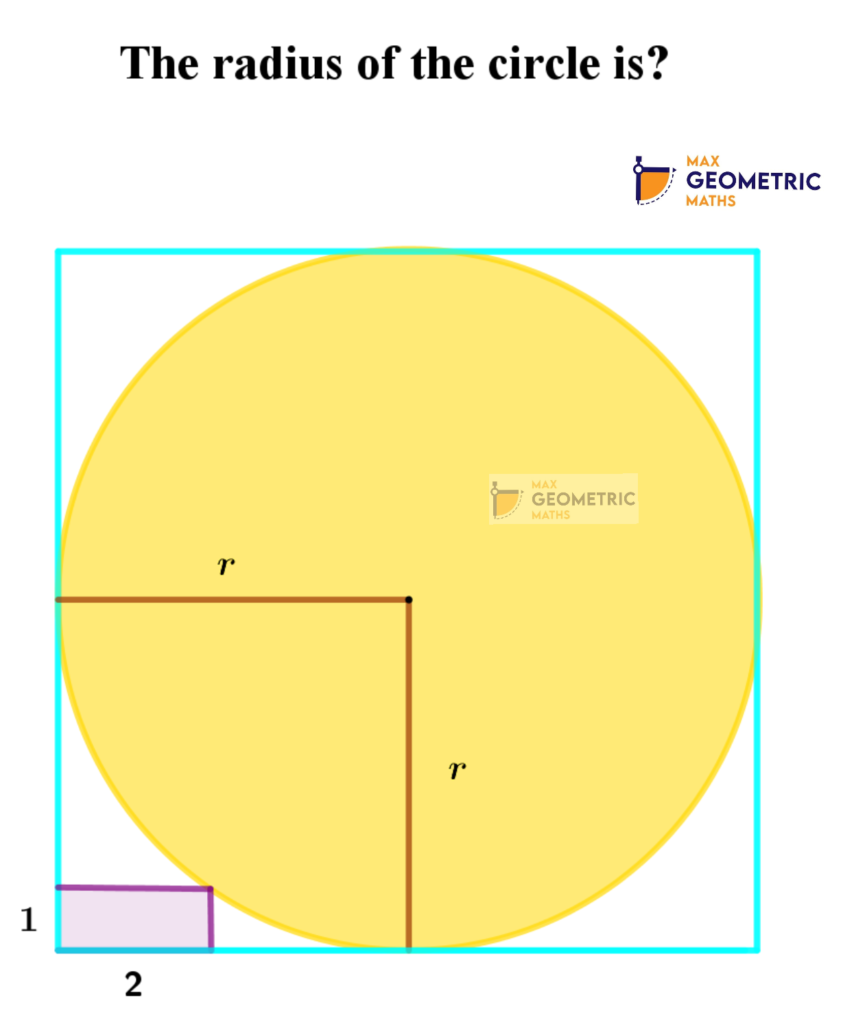
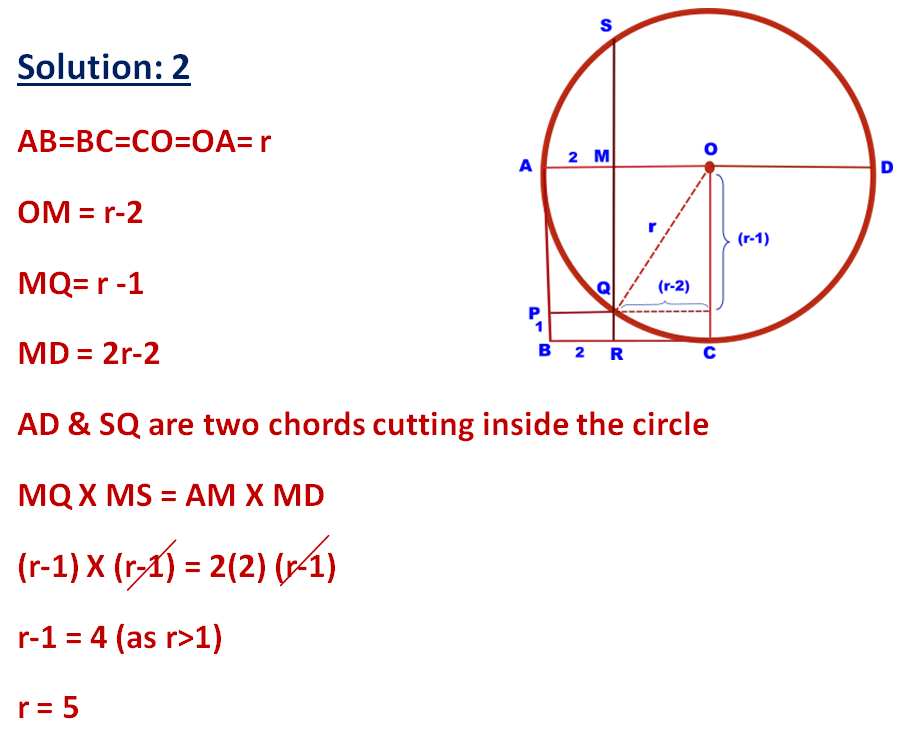
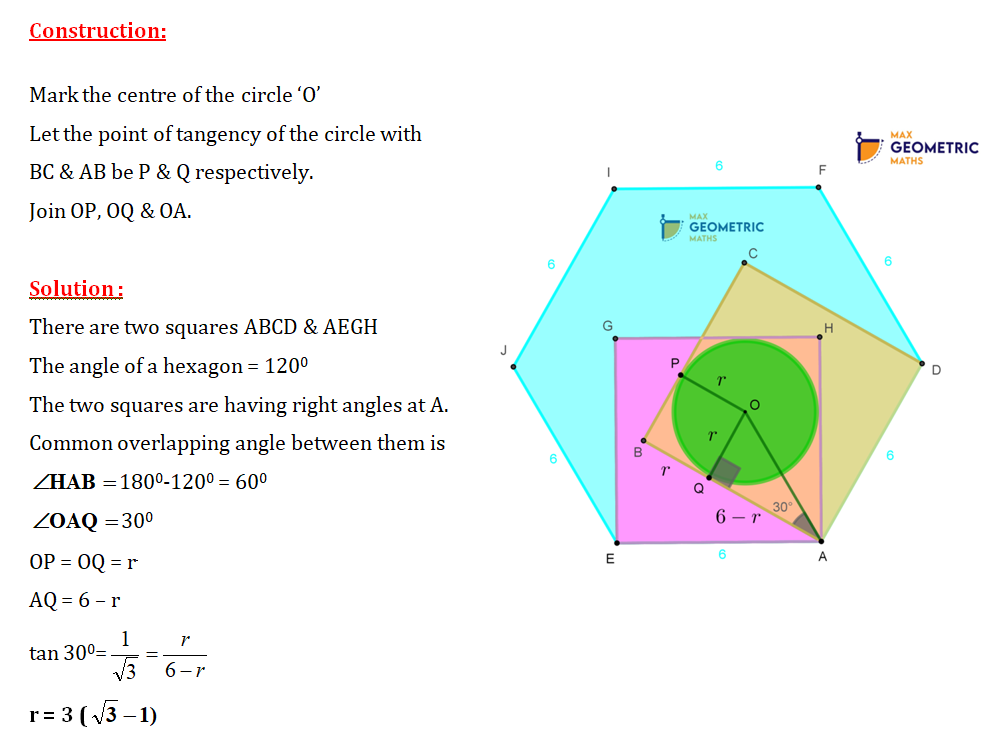
If the side of the regular hexagon is 6cm, the find the radius of the circle
4. Question:
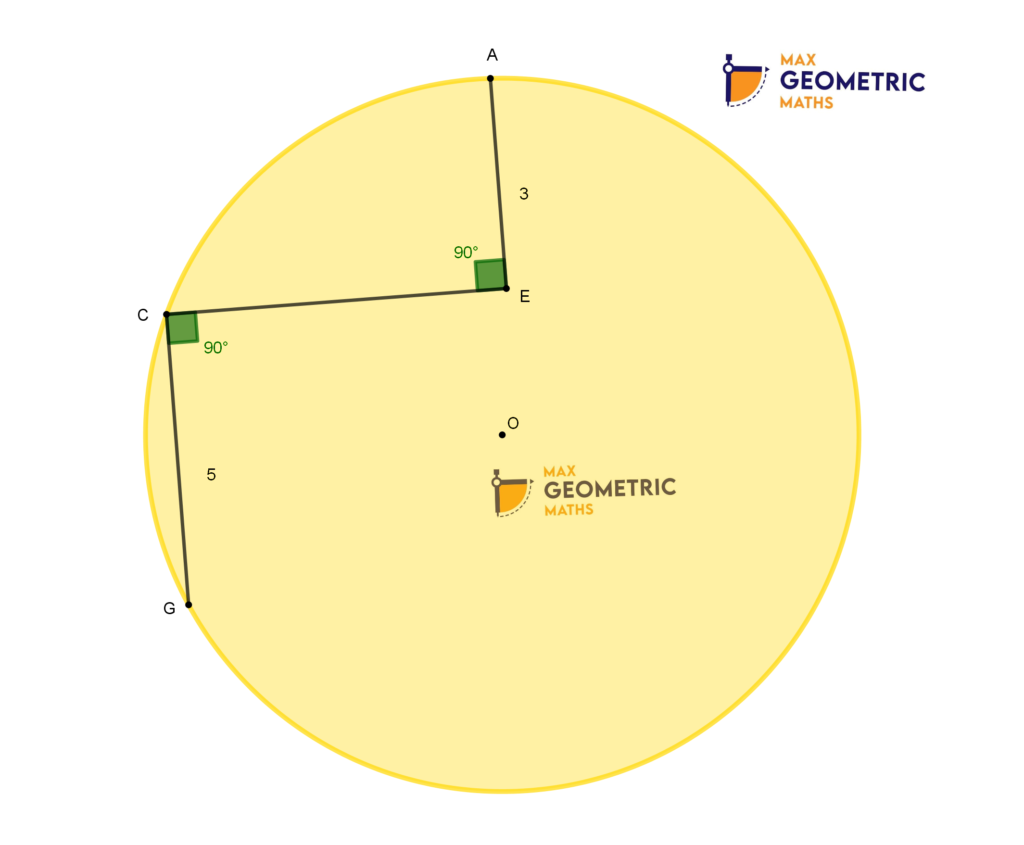
Find the radius of the circle if AE = 3cm, CG = 5cm, AE ⊥ CE & CE ⊥ CG.
5. Question:
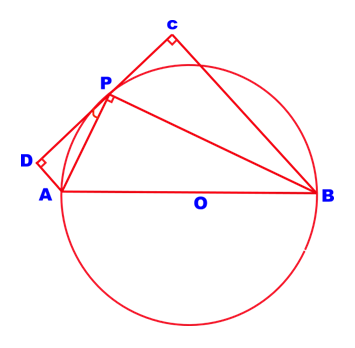
Δ APB is a right angled triangle & O is the circumcentre of the triangle and a tangents drawn at P. From A & B perpendiculars are drawn to meet the tangent at D & C respectively.
Prove that AD + BC = AB
6. Question:
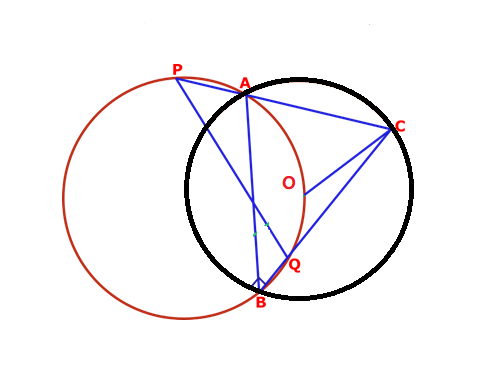
ABC be an acute angled triangle and O be its circumcentre. A circle through the points A, O and B is drawn and CA produced and CB meets the circle at P, Q respectively. Prove that CO & PQ are perpendicular to each other.
7. Question:

ABC is a triangle inscribed in a circle. M is the mid point of major arc AB and D is the foot of the perpendicular from M on AC. Then prove that AD = BC + CD.
8. Question:
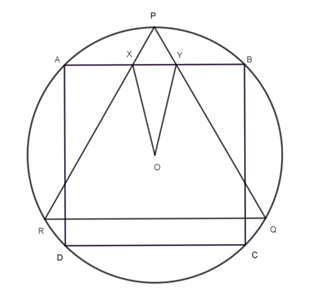
A square ABCD and an equilateral triangle PQR are inscribed in a circle centered at O in such a way that AB is parallel to QR. The sides PQ and PR of the triangle meet the side AB of the square at X and Y respectively. Find the value of ∠XOY.
9. Question: